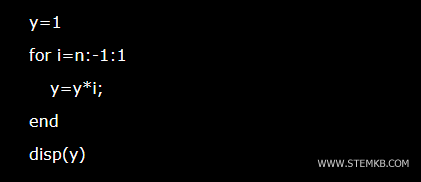Rekursive Funktionen in Matlab

In der Welt der Programmierung sind rekursive Funktionen ein faszinierendes Thema. Speziell in Matlab bieten sie spannende Lösungswege. Lassen Sie uns einen Blick darauf werfen.

Was versteht man unter Rekursion? Eine rekursive Funktion ruft sich selbst ein- oder mehrere Male auf. Dieses Prinzip ist zentral in der funktionalen Programmierung und erweist sich bei bestimmten Problemstellungen als überaus nützlich.

Ein Beispiel wird das Konzept verdeutlichen.

Stellen Sie sich vor, Sie möchten die Fakultät einer Zahl (n!) berechnen. Eine solche rekursive Funktion könnte wie folgt aussehen:

function y = fact(x)
if (x<0)
disp("negative Zahl")
return;
end
if (x<2)
y=1;
return;
else
y=x*fact(x-1);
end
end

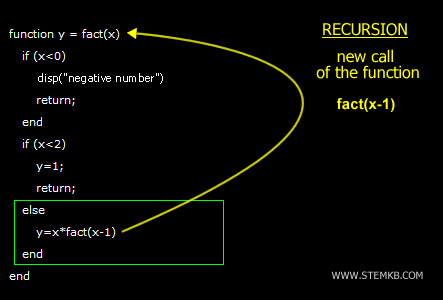
Die Funktion fact() ist rekursiv, da sie sich im Ausdruck y = x * fact(x - 1) selbst aufruft.

Die Funktionsweise ist wie folgt:

Zunächst empfängt die Funktion fact() eine Zahl x als Eingabe. Die weitere Verarbeitung erfolgt in Schritten:

• Bei x<0
  Eine negative Zahl führt zu keinem Ergebnis, da die Fakultät einer solchen nicht definiert ist. In diesem Fall gibt die Funktion eine Meldung aus und beendet den Prozess.
  
• Bei 0≤x<2
  Liegt x zwischen 0 und 2, gibt die Funktion 1 zurück. Hier endet die Rekursion, da kein weiterer Aufruf erfolgt.
  
• Bei x≥2
  Ist x größer oder gleich 2, wird x mit dem Ergebnis von fact(x - 1) multipliziert, wodurch die Funktion sich rekursiv selbst aufruft.
  

Betrachten wir ein konkretes Beispiel: die Funktion fact() mit der Zahl x = 6.

n=6;
y=fact(n);
disp(y)

function y = fact(x)
if (x<0)
disp("negative Zahl")
return;
end
if (x<2)
y=1;
return;
else
y=x*fact(x-1);
end
end

Hinweis: In Matlab muss eine Funktion stets am Ende des Skripts definiert werden.

Die Funktion nimmt die Zahl 6 entgegen und berechnet die Fakultät 6! rekursiv. Sie ruft sich dabei fünfmal mit jeweils kleineren Werten auf.

fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)

Im letzten Schritt gibt fact(1) den Wert 1 zurück, was die vorherigen rekursiven Aufrufe abschließt.

Wenn fact(1) = 1 ist, dann ist fact(2) = 2, weil fact(2) = 2 * fact(1) = 2 * 1 = 2.

fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2

Wenn fact(2) = 2 ist, dann ergibt sich fact(3) als 6, da fact(3) = 3 * fact(2) = 3 * 2 = 6.

fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6

Bei fact(3) = 6 ist fact(4) gleich 24, denn fact(4) = 4 * fact(3) = 4 * 6 = 24.

fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24

Da fact(5) = 5 * fact(4) ist und wir fact(4) als 24 bestimmt haben, muss fact(5) 120 sein.

fact(6)=6*fact(5)
fact(5)=5*fact(4)=5*24=120

Und wenn fact(5) 120 ist, dann ergibt sich fact(6) als 6 * 120 = 720.

fact(6)=6*fact(5)=6*120=720

So ergibt sich also das Ergebnis!

$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$

Die Fakultät von 6 beträgt 720.

720

Hinweis: In diesem Beispiel haben wir eine rekursive Funktion zur Berechnung der Fakultät einer Zahl erstellt. Dies veranschaulicht, wie Rekursion funktioniert. Sie können jedoch auch die vordefinierte Funktion factorial(x) in Matlab verwenden, um die Fakultät ohne Definition einer weiteren Funktion zu berechnen.

factorial(6)=720

Die Fakultät einer Zahl lässt sich auch mit einer iterativen Funktion ohne Rekursion berechnen. In beiden Fällen ist das Endergebnis gleich.

Hier ist ein Beispielalgorithmus zur Berechnung der Fakultät mit Iteration: