Zufallsverteilungen in Matlab
In dieser Lektion werde ich erklären, wie man Wahrscheinlichkeitsverteilungen verwendet, um Zufallszahlen zu generieren.
Warum Verteilungen ändern? Matlab ermöglicht es Ihnen, Zufallszahlen mit verschiedenen Wahrscheinlichkeitsverteilungen zu erzeugen (exponentiell, normal, Poisson, Gamma). Die Wahl der Verteilung hängt davon ab, was Sie simulieren möchten. Einige reale Phänomene lassen sich besser mit einer Verteilung als mit einer anderen simulieren.
Lassen Sie uns einige praktische Beispiele betrachten.
Generieren Sie eine Pseudozufallszahl mit der Funktion rand() oder randi()
>> rand(1)
In diesen Fällen verwendet Matlab die Standard-Gleichverteilung, bei der alle Werte gleichmäßig unter allen möglichen Werten verteilt sind.
Zum Beispiel, erzeugen Sie eine 100x100-Matrix mit Zufallswerten zwischen 0 und 1 und weisen Sie sie der Variablen x zu
Dieser Befehl generiert zehntausend Zufallswerte.
>> x=rand(100);
Visualisieren Sie nun die Verteilung der Werte mit einem Histogramm mit der Funktion hist()
>> hist(x)
Die von Ihnen gerade generierten Zufallswerte sind gleichmäßig zwischen 0 und 1 verteilt.
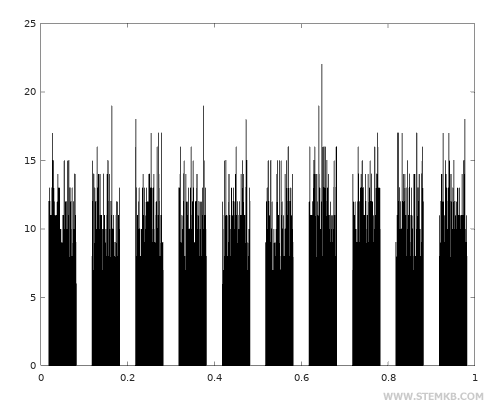
Hinweis. In der Grafik zeigt die horizontale Achse die Zufallswerte von 0 bis 1, was der Bereich der möglichen Werte ist. Die vertikale Achse misst die Häufigkeit, mit der sich Werte wiederholen. Die Häufigkeit ist für jeden Wert ungefähr gleich.
Wenn Sie andere Wahrscheinlichkeitsverteilungen verwenden, sieht das Ergebnis ganz anders aus.
Die Exponentialverteilung
Um Zufallszahlen mit der Exponentialverteilung zu generieren, müssen Sie die Funktion exprnd() verwenden
>> exprnd(1)
ans = 0.90844
Zum Beispiel tippen Sie exprnd(1,3,2), um eine 3x2-Matrix mit Zufallswerten zu erzeugen, die die Exponentialverteilung mit einem Mittelwert von 1 verwenden.
>> exprnd(1,3,2)
ans =
1.09340 0.28265
0.10781 1.72641
0.20653 0.87235
Was ändert sich im Vergleich zur Gleichverteilung?
Um zu verstehen, generieren Sie eine 100x100 Zufallsmatrix mit der Funktion exprnd()
>> x=exprnd(1,100,100);
Dann visualisieren Sie die von Ihnen gerade generierten Zufallswerte mit einem Häufigkeitshistogramm mit der Funktion hist()
>> hist(x)
In der Exponentialverteilung sind die Zufallswerte am Anfang des Bereichs der möglichen Werte konzentriert.
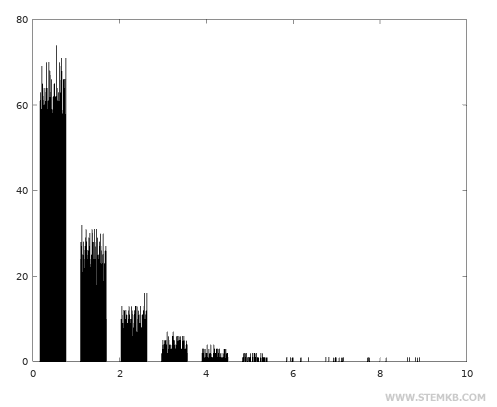
In diesem Fall sind Werte nahe Null oder dem Anfangswert des Bereichs viel häufiger.
Die Häufigkeit nimmt exponentiell in höheren Werten ab.
Die Normalverteilung
Um Zufallszahlen mit der Normalverteilung zu generieren, verwenden Sie die Funktion randn()
>> randn(1)
ans = 0.85251
Zum Beispiel tippen Sie randn(2,3), um eine 2x3 Zufallsmatrix zu erstellen
>> randn(2,3)
ans =
-0.32674 2.24641 -0.19528
-0.37856 0.13721 0.41417
Generieren Sie jetzt eine 100x100-Matrix mit Zufallswerten mit der Normalverteilung
>> x=randn(100);
Dann visualisieren Sie das Häufigkeitshistogramm der Zufallswerte mit der Funktion hist()
>> hist(x)
In der Normalverteilung sind die häufigsten Werte innerhalb des Bereichs der möglichen Werte zentriert.
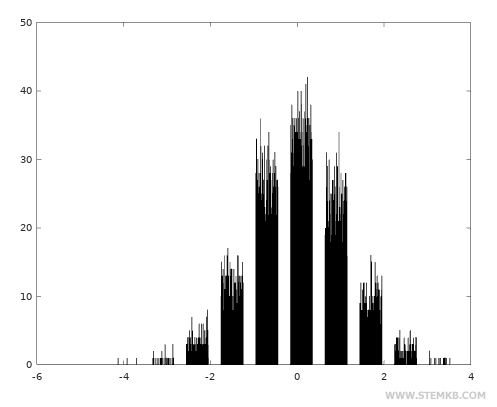
Die Häufigkeit der Zufallswerte nimmt ab, wenn man sich von Null entfernt, sowohl nach rechts als auch nach links.
Die Normalverteilung ist durch eine glockenförmige Kurve gekennzeichnet.
Die Poisson-Verteilung
Um Zufallszahlen mit der Poisson-Verteilung zu generieren, können Sie die Funktion poissrnd() verwenden.
>> poissrnd(1)
ans = 3
Die Poisson-Verteilung erzeugt Zufallszahlen um einen Mittelwert herum.
Beispiel. Wenn der Parameter der Funktion poissrnd(1) auf 1 gesetzt wird, erzeugt sie Zufallszahlen aus einer Poisson-Verteilung mit einem Durchschnittswert von 1.
Zum Beispiel können Sie poissrnd(5,2,3) eingeben, um eine 2x3 Zufallsmatrix zu erstellen, die aus Werten um den Mittelwert von 5 besteht.
>> poissrnd(5,2,3)
ans =
3 7 6
5 2 2
Sie können auch eine 100x100 Zufallsmatrix mit Werten um den Mittelwert von 5 erstellen.
>> x=poissrnd(5,100,100)
Dann können Sie das Häufigkeitshistogramm mit der Funktion hist() anzeigen.
>> hist(x)
In der Poisson-Verteilung konzentrieren sich die Zufallswerte in der Regel um den Mittelwert von 5.
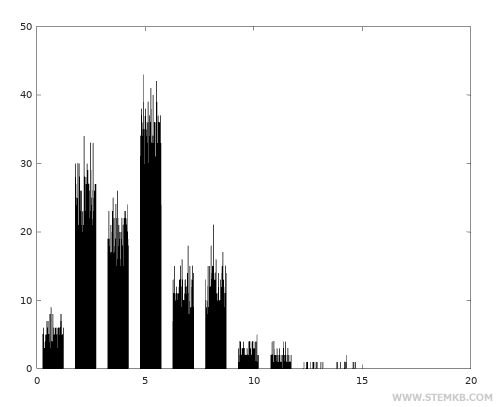
Die Gamma-Verteilung
Um Zufallszahlen mit der Gamma-Verteilung zu erzeugen, können Sie den Befehl randg() verwenden.
>> randg(1)
ans = 2.5621
Zum Beispiel können Sie randg(100,2,3) eingeben, um eine 2x3 Zufallsmatrix um den zentralen Wert von 100 zu erzeugen.
>> randg(100,2,3)
ans =
101.843 98.346 87.956
93.809 99.350 93.122
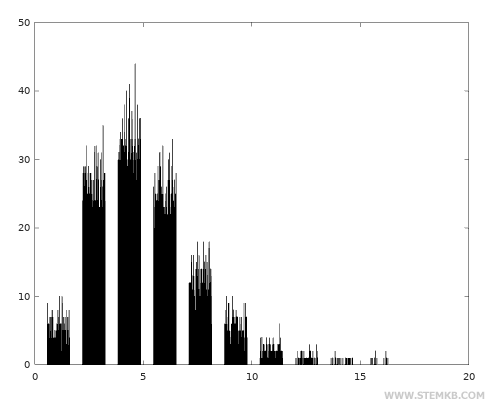
Sie können auch eine 100x100 Zufallsmatrix mit der Gamma-Verteilung um den zentralen Wert von 5 erzeugen.
>> x = randg(5,100,100)
Danach können Sie das Histogramm der Häufigkeiten mit der Funktion hist() anzeigen.
>> hist(x)
In der Gamma-Verteilung sind Werte in der Nähe des zentralen Wertes häufiger.
Indem Sie diese Wahrscheinlichkeitsverteilungen in MATLAB verwenden, können Sie Zufallszahlen mit verschiedenen Eigenschaften erzeugen.
Diese Funktionen können verwendet werden, um einzelne Zufallswerte, Vektoren oder Matrizen aus Zufallswerten zu generieren.