Integralrechnung mit GeoGebra

In unserem heutigen Tutorial widmen wir uns der Berechnung unbestimmter Integrale mit GeoGebra, illustriert durch ein detailliertes Beispiel.

Beginnen wir mit den Grundlagen: Was versteht man unter einem unbestimmten Integral? Die Integration einer Funktion, beispielsweise f(x), führt uns zu einer neuen Funktion, g(x)+k, $$ \int f(x) = g(x) + k $$, deren Ableitung D[g(x)+k] uns wieder zur Ausgangsfunktion f(x) bringt. $$ D_t[ g(x) + k ] = f(x) $$

Zuerst geben Sie eine Funktion in GeoGebra ein. Für unsere Demonstration wählen wir die Funktion f(x)=x².

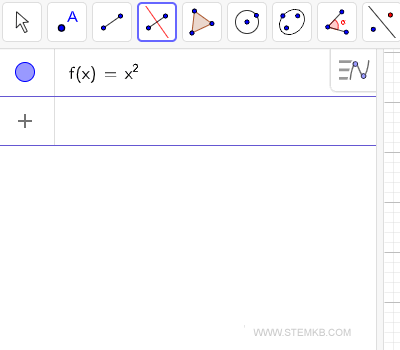
Verwenden Sie anschließend den Befehl Integral().

Im Befehl geben Sie die zu integrierende Funktion an, die wir in diesem Beispiel einfach „f“ nennen.

GeoGebra führt daraufhin die Berechnung durch und zeigt das unbestimmte Integral in der Form g(x)=1/3·x³ für die gewählte Funktion f(x) an.

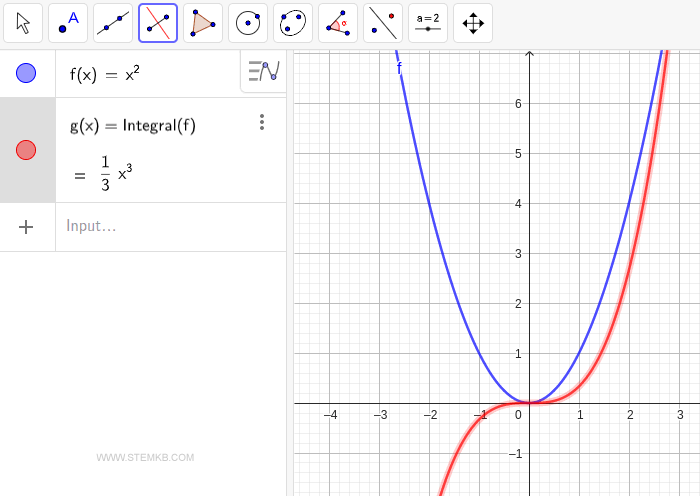
Es ist wesentlich zu erkennen, dass das Ergebnis eines unbestimmten Integrals keine einzelne Funktion g(x) ist, sondern vielmehr eine Familie von Funktionen, g(x)+k, darstellt, wobei k eine beliebige Konstante ist. Genauer gesagt, sollte es als g(x)=1/3·x³+k formuliert werden. Dies beruht auf der Tatsache, dass die Ableitung einer Konstanten k stets null ist, d.h., D[k] = 0. Daraus folgt, dass Ableitungen wie D[1/3·x³+2] oder D[1/3·x³+3] stets zur Ausgangsfunktion f(x)=x² zurückführen.

Benötigen Sie eine Bestätigung?

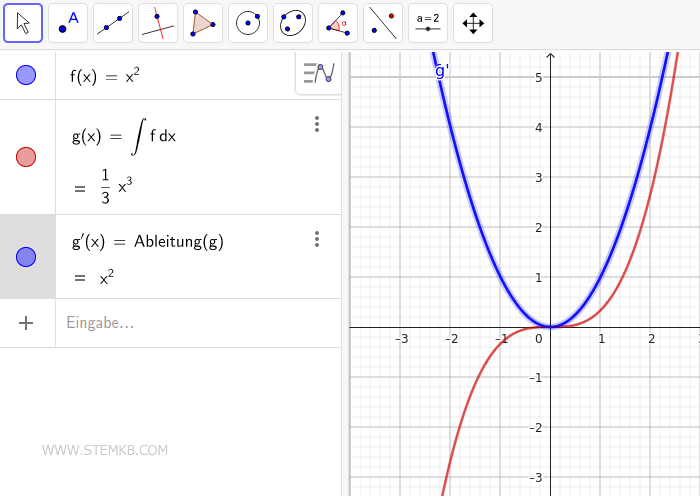
Überprüfen Sie Ihre Ergebnisse, indem Sie die Ableitung mit dem Befehl Ableitung() berechnen.

Bei der Berechnung der ersten Ableitung für g(x)=1/3·x³ gelangen wir zurück zu unserer Anfangsfunktion f(x)=x², was bestätigt, dass die Differenzierung die Umkehrung der Integration darstellt.

Wenn Sie diesen Leitfaden hilfreich fanden, empfehlen wir Ihnen, unsere weiteren Tutorials zu erkunden, um noch tiefere Einblicke zu gewinnen.