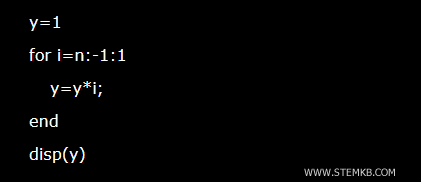Rekursive Funktionen in Octave
In dieser Lektion werde ich erklären, wie man Rekursion in Funktionen in Octave verwendet.
Rekursion bezieht sich auf die Technik, dass eine Funktion sich selbst mehrere Male aufruft. Es ist ein grundlegendes Konzept in der funktionalen Programmierung.
Um Ihnen dieses Konzept zu verdeutlichen, werde ich Ihnen ein praktisches Beispiel geben.
Sie können Rekursion verwenden, um die Fakultät einer Zahl zu berechnen.
1;
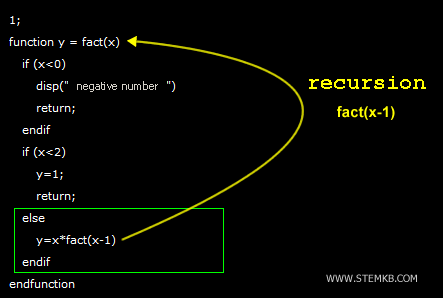
function y = fact(x)
if (x<0)
disp("negative number")
return;
endif
if (x<2)
y=1;
return;
else
y=x*fact(x-1)
endif
endfunction
In diesem Skript habe ich eine Funktion namens fact() definiert, die eine numerische Eingabe (x) entgegennimmt.
- Wenn x<0
Zuerst überprüft die Funktion, ob die Eingabe negativ ist. Wenn x<0 ist, gibt die Funktion eine Nachricht aus, dass die Zahl negativ ist, und beendet den Funktionsaufruf mit der return-Anweisung. Dies liegt daran, dass die Fakultät einer negativen Zahl undefiniert ist.

- Wenn 0≤x<2
Danach überprüft die Funktion, ob die Eingabe kleiner als 2 ist. Wenn 0≤x<2 ist, gibt die Funktion 1 zurück und beendet die Rekursion. Die return-Anweisung sendet den Wert 1 zurück zum vorherigen Funktionsaufruf und schließt damit die rekursive Schleife ab.

- Wenn x≥2
Schließlich multipliziert die Funktion, wenn die Eingabe größer oder gleich 2 ist, die Eingangsnummer x mit dem Ergebnis von fact(x-1). Dies wird durch Rekursion erreicht, bei der sich die Funktion selbst mit einer neuen Eingabe von x-1 aufruft, was die aktuelle ganze Zahl x um eins reduziert. Der Vorgang wiederholt sich, bis der Basisfall von x<2 erreicht ist und die Rekursion beendet wird.
Insgesamt bietet diese Funktion eine effiziente Möglichkeit, die Fakultät von nicht-negativen Ganzzahlen zu berechnen.
Beispielsweise können Sie die gerade erstellte fact()-Funktion aufrufen und 6 als anfänglichen Parameter übergeben.
Die Funktion nimmt die Eingangsnummer x=6 und berechnet rekursiv die Fakultät.
n=6
y=fact(n);
disp(y)
Das Skript gibt die Zahl 720 aus, die die Fakultät von 6! ist.
720
Warum ist die Ausgabe der Funktion 720?
Die Funktion ruft sich fünfmal selbst auf (Rekursion), indem sie eine progressiv kleinere Zahl übergibt.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
Im letzten Aufruf fact(1)=1 gibt die Funktion 1 zurück, weil der Eingabewert (x=1) kleiner als zwei ist.
An diesem Punkt endet die Rekursion und der Prozess kehrt rückwärts zurück, indem alle vorherigen Aufrufe geschlossen werden.
Wenn fact(1)=1, dann ist fact(2)=2, weil fact(2)=2*fact(1)=2*1=2
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2
Wenn fact(2)=2, dann ist fact(3)=6, weil fact(3)=3*fact(2)=3*2=6
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6
Wenn fact(3)=6, dann ist fact(4)=24, weil fact(4)=4*fact(3)=4*6=24
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24
Wenn fact(4)=24, dann ist fact(5)=120, weil fact(5)=5*fact(4)=5*24=120
fact(6)=6*fact(5)
fact(5)=5*fact(4)=5*24=120
Wenn fact(5)=120, dann ist fact(6)=720, weil fact(6)=6*fact(5)=6*120=720
fact(6)=6*fact(5)=6*120=720
Daher ist die Fakultät von 6! gleich 720.
$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$
Hinweis. In diesem Beispiel habe ich eine Faktorielfunktion erstellt, um zu erklären, wie Rekursion in Octave funktioniert. Wenn Sie jedoch nur das Faktoriel einer Zahl berechnen möchten, sollten Sie beachten, dass Octave auch eine spezielle vordefinierte Funktion factorial(x) hat, die viel bequemer zu verwenden ist. Darüber hinaus können Sie das Faktoriel auch durch die Entwicklung einer Funktion basierend auf Iteration ohne Verwendung von Rekursion berechnen, und das Ergebnis ist immer dasselbe.