Berechnung der inversen Matrix mit Geogebra
In dieser Lektion zeige ich Ihnen, wie Sie mit Geogebra die inverse Matrix berechnen können.
Was versteht man unter einer inversen Matrix? Eine Matrix A ist invertierbar, wenn es eine inverse Matrix B gibt, die mit A multipliziert eine Einheitsmatrix ergibt.
Beginnen wir mit dem Erstellen einer invertierbaren quadratischen Matrix.
Als Beispiel nehmen wir eine 3x3 Matrix mit drei Zeilen und drei Spalten.
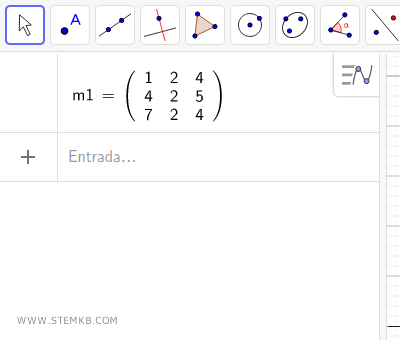
Zu beachten: Falls Sie mit diesem Vorgang nicht vertraut sind, empfehle ich Ihnen, unsere vorherige Lektion zur Erstellung einer Matrix in Geogebra durchzulesen.
Geben Sie nun die Funktion Invertiere() in ein neues Feld in Geogebra ein.
Tragen Sie den Namen der Matrix, die Sie soeben erstellt haben, in die runden Klammern ein.
Geogebra führt die Berechnung durch und zeigt die inverse Matrix an.
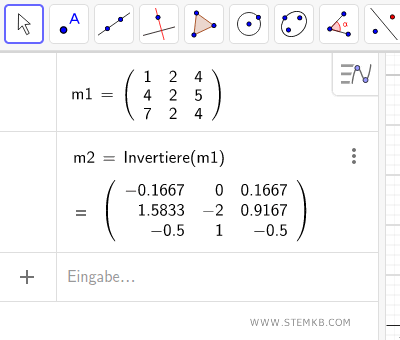
Die inverse Matrix wurde erfolgreich berechnet.
Zur schnellen Überprüfung multiplizieren Sie die ursprüngliche Matrix (invertierbar) mit der ermittelten inversen Matrix.
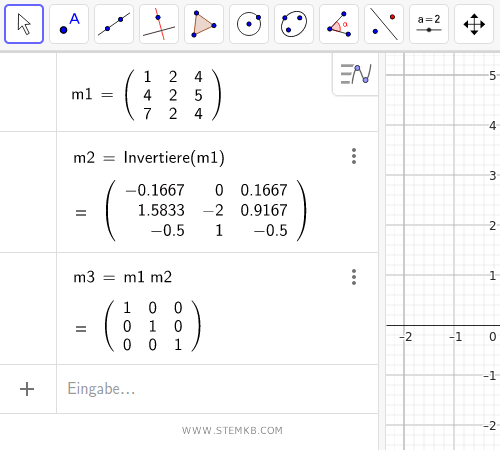
Das Ergebnis dieses Produkts ist die Einheitsmatrix, charakterisiert durch Einsen auf der Hauptdiagonale und Nullen in allen anderen Positionen.
Wenn Sie diese Anleitung von StemKB hilfreich fanden, bleiben Sie weiterhin dabei für mehr hilfreiche Tipps und Anleitungen.