Berechnung des Rangs einer Matrix in Geogebra

In diesem Tutorial erfahren Sie, wie der Rang einer quadratischen Matrix in Geogebra bestimmt wird.

Was versteht man unter dem Rang einer Matrix? Der Rang ist die höchste Ordnung der quadratischen Untermatrizen innerhalb der Matrix, die einen nicht-null Determinantenwert aufweisen.

Geben Sie eine quadratische Matrix ein.

Zum Beispiel könnte dies eine 3x3-Matrix mit drei Zeilen und Spalten sein.

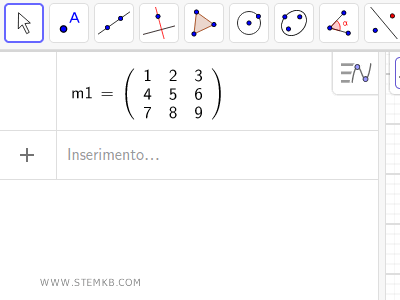
Hinweis: Wenn Sie nicht sicher sind, wie Sie eine Matrix in Geogebra erstellen können, empfehlen wir Ihnen, unsere Anleitung zur Erstellung einer Matrix in Geogebra durchzulesen.

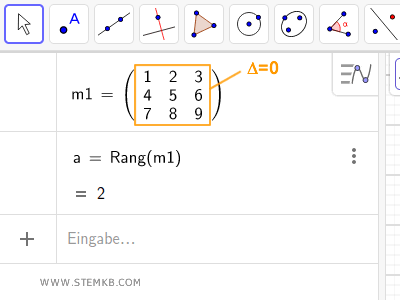
Nutzen Sie die Funktion Rang(), um den Rang der Matrix zu ermitteln.

Tragen Sie den Namen Ihrer Ausgangsmatrix in die runden Klammern ein.

Geogebra führt die Berechnung durch und zeigt den Rang der Matrix an.

Erklärung: Der Rang dieser Matrix ist 2, da der Determinant der 3x3-Matrix Δ (m1) = 0 beträgt und somit nicht drei sein kann.

Mindestens eine 2x2-Untermatrix weist einen Determinantenwert ungleich null auf, wie beispielsweise die blau markierte Untermatrix mit dem Determinantenwert Δ = -2.

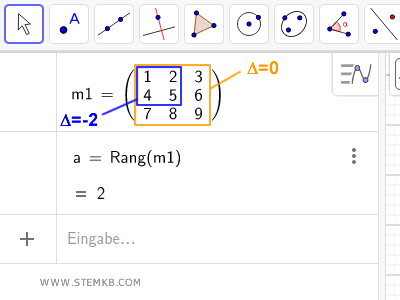
Diese blaue Untermatrix ist von zweiter Ordnung, da sie aus zwei Zeilen und Spalten besteht. Folglich ist die höchste Ordnung unter den Untermatrizen mit einem Determinantenwert ungleich null zwei. Andere mögliche Untermatrizen hätten eine Ordnung, die gleich oder geringer als die soeben ermittelte ist.

Wenn Sie diese Einleitung hilfreich fanden, bleiben Sie weiterhin für mehr Einblicke und Anleitungen mit uns.