Das Kreuzprodukt in Geogebra

In diesem Lernprogramm führe ich Sie durch die Berechnung des Kreuzprodukts zweier Vektoren mittels Geogebra.

Beginnen Sie, indem Sie zwei Vektoren im dreidimensionalen Raum erstellen.

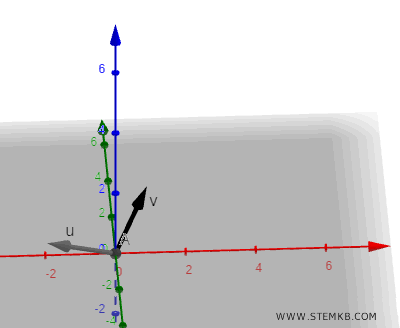
Die Koordinaten des ersten Vektors lauten wie folgt:

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} $$

Und für den zweiten Vektor:

$$ \vec{u} = \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix} $$

Falls Sie nicht sicher sind, wie Sie einen Vektor erstellen können, empfehlen wir Ihnen, unsere Online-Lektion über die Erstellung von Vektoren mit Geogebra zu konsultieren.

Geben Sie anschließend Kreuzprodukt(v,u) in das Befehlsfeld von Geogebra ein und bestätigen Sie mit Enter.

Die Bezeichnungen u und v stehen hier für die Namen der gerade von Ihnen erstellten Vektoren.

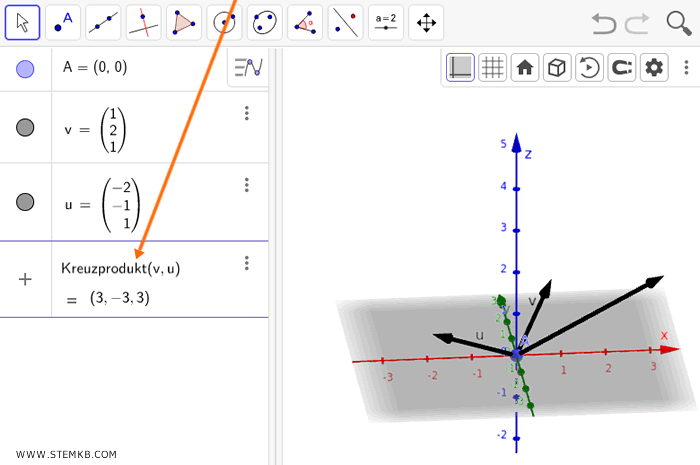
Geogebra wird nun das Kreuzprodukt Ihrer Vektoren berechnen und anschaulich darstellen.

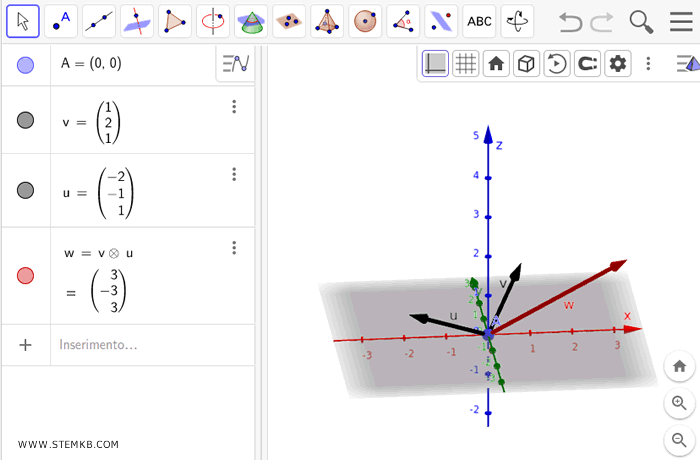
Für dieses Beispiel ergibt sich das Kreuzprodukt als Vektor w mit den folgenden Koordinaten:

$$ \vec{u} = \begin{pmatrix} 3 \\ -3 \\ 3 \end{pmatrix} $$

Warum ist das Kreuzprodukt von Bedeutung? Das Kreuzprodukt zweier Vektoren u und v resultiert in einem dritten Vektor w, der senkrecht zu den beiden ursprünglichen Vektoren steht. Die Ausrichtung dieses resultierenden Vektors wird durch die Reihenfolge der ursprünglichen Vektoren bestimmt. Weisen die Ausgangsvektoren in dieselbe Richtung, resultiert dies in einem Nullvektor. Die Größe des Kreuzprodukts gibt die von den beiden Vektoren auf ihrer gemeinsamen Ebene aufgespannte Fläche an.

Wenn Sie diese praxisnahe Anleitung von StemKB schätzen, freuen Sie sich auf weitere.