Skalarprodukt mit GeoGebra berechnen

Diese Anleitung führt Sie durch die notwendigen Schritte, um das Skalarprodukt zweier Vektoren mit GeoGebra zu berechnen.

Beginnen Sie damit, zwei Vektoren vom Ursprung aus zu erstellen, die als u und v bezeichnet werden.

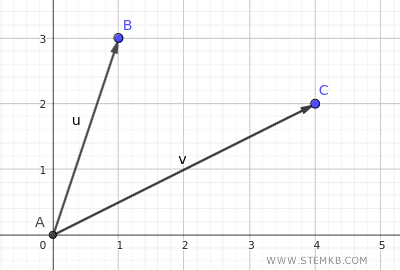
Falls Ihnen die Erstellung eines Vektors kompliziert erscheint, keine Sorge. In einem anderen Tutorial habe ich die Grundlagen zur Erstellung eines Vektors mit GeoGebra erläutert.

Öffnen Sie ein neues GeoGebra-Arbeitsblatt und geben Sie Skalarprodukt(u,v) ein.

Ersetzen Sie u und v durch die Namen Ihrer neu erstellten Vektoren.

Drücken Sie die Eingabetaste und voilà!

GeoGebra berechnet mühelos das Skalarprodukt Ihrer Vektoren.

In unserem Fall ergibt das Skalarprodukt 10.

Warum sich mit dem Skalarprodukt beschäftigen? Über seine Bedeutung in der Vektorrechnung hinaus, reduziert das Skalarprodukt die Beziehung zweier Vektoren auf eine einzige, aufschlussreiche Zahl. Es wird deshalb als "skalar" bezeichnet. Ein Skalarprodukt von Null? Das bedeutet, Ihre Vektoren sind orthogonal und schneiden sich in einem exakten 90° Winkel. Neugierig auf mehr? Tauchen Sie tiefer in das Thema Skalarprodukt hier ein.

Sie können das Skalarprodukt in GeoGebra auch einfach mit u*v aufrufen

Das Ergebnis bleibt dasselbe.

Hat Ihnen diese Anleitung gefallen? Bleiben Sie dran für weitere Einsichten und Tutorials.