Komplexe Konjugation in Octave
In dieser Lektion werde ich erklären, wie man in Octave das konjugierte einer komplexen Zahl findet.
Was ist das komplexe Konjugat? Das Konjugat einer komplexen Zahl z=a+bi ist eine komplexe Zahl, die denselben Realteil hat und bei der das Vorzeichen des Imaginärteils geändert ist. Zum Beispiel hat die komplexe Zahl z1=2+3i das komplexe Konjugat z2=2-3i und umgekehrt.
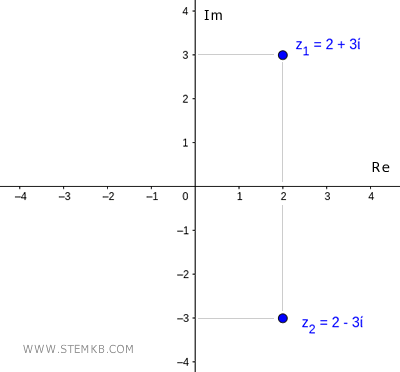
Lassen Sie mich Ihnen ein praktisches Beispiel geben.
Definieren Sie die komplexe Zahl z = 2 + 3i in Octave mit der Funktion complex(2,3).
>> z=complex(2,3)
ans = 2 + 3i
Um das Konjugat einer komplexen Zahl in Octave zu erhalten, können Sie die Funktion conj() verwenden.
Wenn Sie zum Beispiel eine komplexe Zahl z=2+3i haben, können Sie ihr Konjugat finden, indem Sie conj(z) eingeben.
>> conj(z)
ans = 2 - 3i
Die Funktion gibt das Konjugat der komplexen Zahl zurück, in diesem Fall 2 - 3i.
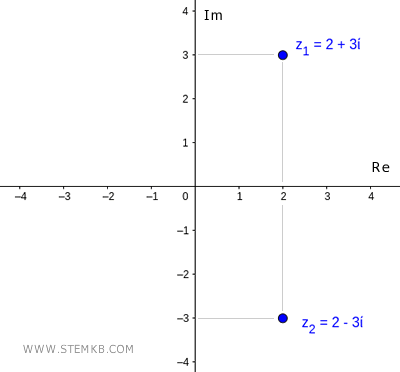
Wofür dient die Berechnung des komplexen Konjugats?
Die Berechnung des komplexen Konjugats vereinfacht bestimmte Operationen in der Arithmetik mit komplexen Zahlen.
Zum Beispiel ist das Produkt einer komplexen Zahl mit ihrem Konjugat gleich dem Quadrat ihres Betrags.
Um dies zu berechnen, multiplizieren Sie die komplexe Zahl z mit ihrem Konjugat conj(z). Das Produkt ist gleich 13.
>> z*conj(z)
ans = 13
Um den Betrag der komplexen Zahl z zu berechnen, können Sie die eingebaute Funktion abs() in Octave verwenden.
Das Ergebnis dieser Funktion auf z angewendet beträgt ungefähr 3.6
>> abs(z)
ans = 3.6056
Darüber hinaus berechnen Sie das Quadrat des Betrags von z.
Das Ergebnis wird immer 13 sein.
>> (abs(z))^2
ans = 13.000
Dies impliziert, dass der Betrag einer komplexen Zahl auch durch die Quadratwurzel des Produkts der komplexen Zahl und ihres Konjugats erhalten werden kann.
>> sqrt(z*conj(z))
ans = 3.6056
Wenn Sie Nigiaras Lektion zur Verwendung von komplexen Zahlen in Octave hilfreich fanden, sollten Sie uns weiterhin folgen, um mehr zu erfahren.
Hinweis. Im Kontext von komplexen Zahlen werden die Begriffe "Betrag" und "Modul" oft synonym verwendet, um den absoluten Wert oder die Entfernung einer komplexen Zahl vom Ursprung der komplexen Ebene zu bezeichnen.