Winkel und Modul einer komplexen Zahl in Octave

In dieser Lektion werde ich erklären, wie man den Winkel (Argument) und das Modul einer komplexen Zahl in Octave berechnet.

Was sind das Modul und der Winkel einer komplexen Zahl? Jede komplexe Zahl z=a+bi kann auf der komplexen Ebene an den Koordinaten (a,b) dargestellt werden.

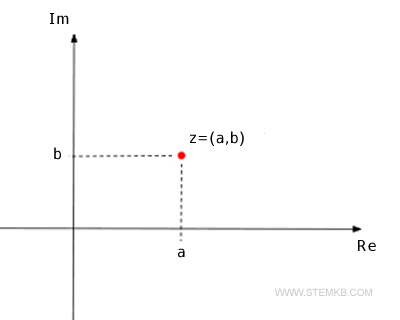
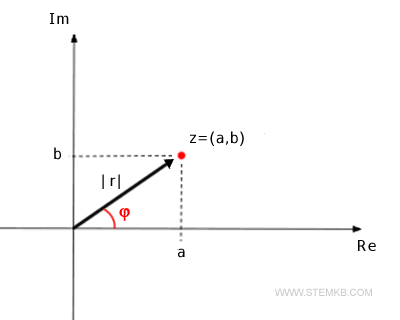
Daher ist jeder Punkt auf der Ebene eine andere komplexe Zahl und kann eindeutig vom Ursprung aus durch einen Vektor erreicht werden. Die Länge r=|z| des Vektors wird als das Modul der komplexen Zahl z bezeichnet. Der Winkel φ des Vektors, der gegen den Uhrzeigersinn von der positiven reellen Achse (Re) gemessen wird, wird als Argument der komplexen Zahl bezeichnet.

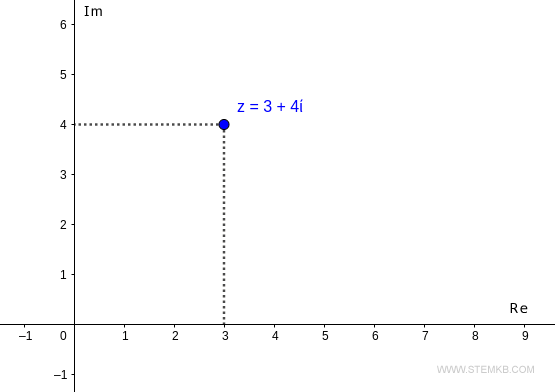
Zum Beispiel betrachten wir die komplexe z=3+4i

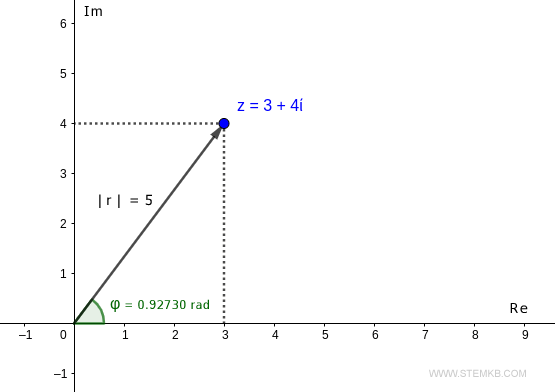
Zahl z=3+4i. Auf der komplexen Ebene befindet sich die Zahl z an dem Punkt mit den Koordinaten (3,4).

Dieser Punkt ist nur durch einen Vektor der Länge r und des Winkels φ vom Ursprung aus erreichbar.

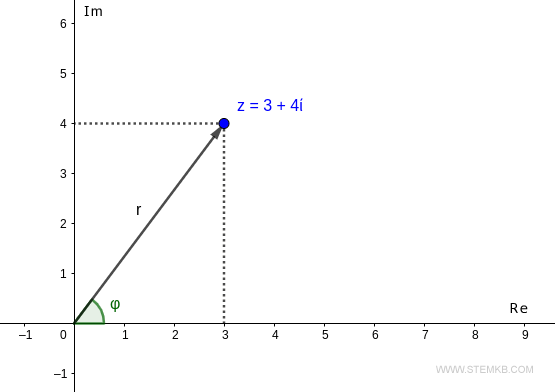
Um das Modul r=|z| der komplexen Zahl zu berechnen, welches die Länge des Vektors darstellt, benutzt man die Funktion abs() in Octave.

>> abs(z)
ans= 5

Daher ist das Modul der komplexen Zahl z=3+4i gleich 5.

Mit anderen Worten hat der Vektor, der den Ursprung mit dem Punkt (3,4) verbindet, eine Länge von fünf.

Um den Winkel (das Argument) der komplexen Zahl zu berechnen, benutzt man stattdessen die Funktion angle().

>> angle(z)
ans = 0.92730

Octave gibt den Winkel in Radiant zurück.

In diesem Fall beträgt das Argument der komplexen Zahl z=3+4i 0,92730 Radiant, was ungefähr 53 Grad entspricht.

Wenn diese Lektion zu Octave von Nigiara hilfreich ist, folgen Sie uns weiterhin.