Die Länge eines Vektors in Octave bestimmen

In dieser Lektion möchte ich Ihnen zeigen, wie Sie die Länge eines Vektors in Octave berechnen können.

Zunächst einmal, was verstehen wir unter der Länge eines Vektors? Es handelt sich dabei um die euklidische Länge des Vektors, die auch als Norm bezeichnet wird. Wenn wir beispielsweise von der euklidischen Norm eines Vektors sprechen, meinen wir die Länge des Pfeiles.

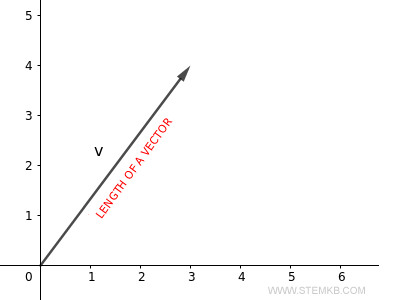
Lassen Sie mich dies an einem praktischen Beispiel verdeutlichen.

Wir definieren einen Vektor in der Variable V:

>> V=[3 4]
V =
3 4

Das entspricht einem Vektor mit dem Endpunkt bei (3;4).

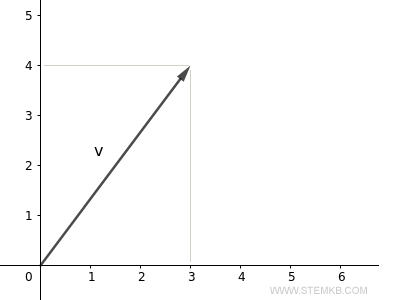
Um die Länge des Vektors (oder seine Größe bzw. Norm) zu bestimmen, geben Sie die Funktion norm(V) ein.

>> norm(V)
ans = 5

Die Länge (oder Norm) des Vektors beträgt also 5.

Das entspricht der Länge des Pfeils in der kartesischen Ebene.

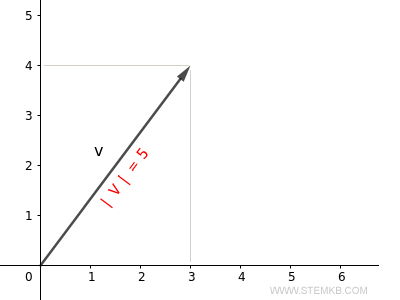
Überprüfung. Die Länge eines Vektors (sein Modul) kann auch mit dem Satz des Pythagoras berechnet werden $$ | \vec{v} | = \sqrt{3^2+4^2} = \sqrt{25} = 5 $$ Die Länge des Vektors ist also 5. Das Ergebnis stimmt.