Einen Vektor in Octave erstellen
In dieser Lektion erkläre ich, wie man Vektoren in Octave mit einem praktischen Beispiel definiert.
Zum Beispiel hat der Vektor v(2; 4) zwei Dimensionen
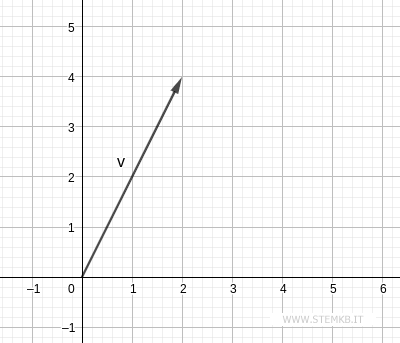
Der Vektor hat zwei Komponenten x = 2 und y = 4.
Um diesen Vektor in Octave zu definieren, verwenden Sie eine Array-Variable und trennen die Komponenten des Vektors mit Semikolons.
>> v=[2;4]
Dies erstellt einen Spaltenvektor
$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Nachdem Sie den Vektor erstellt haben, können Sie ihn in jeder Vektorberechnungsoperation verwenden (Summe, Vektorprodukt, Skalarprodukt usw.)
Wie man einen Vektor im dreidimensionalen Raum erstellt
Ähnlich können Sie einen Vektor mit drei oder mehr Komponenten erstellen.
Zum Beispiel der Vektor v(2;4;3).
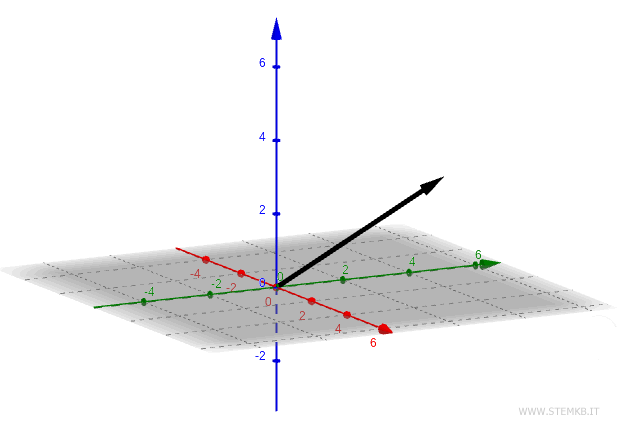
Dieser Vektor hat drei Komponenten x = 2, y = 4, z = 3
$$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix} $$
Um diesen Vektor in Octave zu definieren, geben Sie ein
>> v=[2;4;3]
Wie man einen Zeilenvektor erstellt
In den vorherigen Beispielen habe ich Ihnen erklärt, wie man einen Spaltenvektor in Octave definiert.
$$ \vec{v} = \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$
Manchmal jedoch kommt es vor, dass Sie mit einem Zeilenvektor arbeiten müssen. Das ist ein Vektor, dessen Elemente horizontal angeordnet sind.
$$ \vec{v} = \begin{pmatrix} a & b & c \end{pmatrix} $$
Um einen Zeilenvektor in Octave zu erstellen, müssen Sie lediglich die Komponenten durch ein Leerzeichen oder ein Komma trennen.
Zum Beispiel, um diesen Zeilenvektor zu definieren
$$ \vec{v} = \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} $$
Schreiben Sie ein Array und trennen Sie Elemente mit Kommas
>> v=[1, 2, 3]
Das Ergebnis ist ein Zeilenvektor.
Anmerkung. Es gibt auch eine andere Möglichkeit, einen Zeilenvektor zu erstellen. Sobald Sie einen Spaltenvektor erstellt haben, können Sie ihn durch Transposition in einen Zeilenvektor umwandeln.