Erstellung logarithmischer Diagramme in MATLAB

Ich möchte Ihnen die Verwendung von logarithmischen Diagrammen in Matlab näherbringen.

Was versteht man unter einem logarithmischen Diagramm? Es ist ein Diagramm, bei dem die Werte auf einer oder beiden Achsen in einer logarithmischen Skala abgebildet werden. Diese Art von Diagrammen eignet sich hervorragend, um exponentiell variierende Daten zu visualisieren.

Beginnen wir mit einem einfachen Beispiel, um das Prinzip leicht verständlich zu machen.

Wir erstellen ein Array 'x', das ganzzahlige Werte von 1 bis 10 umfasst.

>> x=0:1:10;

Anschließend erstellen wir ein zweites Array, 'y', das die Werte der Funktion y = x² beinhaltet.

>> y=x.^2

Beide Arrays beinhalten jeweils 10 Werte.

Während das 'x'-Array linear ansteigt (1, 2, 3, 4, ...), wächst das 'y'-Array exponentiell (1, 4, 9, 16, ...).

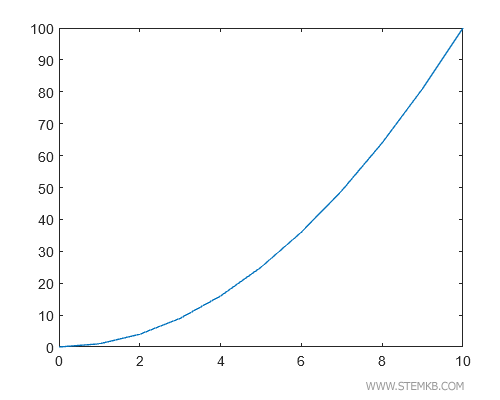
Nun visualisieren wir diese Funktion in einem kartesischen Diagramm, indem wir plot(x, y) eingeben.

>> plot(x,y)

Das Resultat? Eine eindrucksvolle Kurve, die das exponentielle Wachstum von y=x² verdeutlicht.

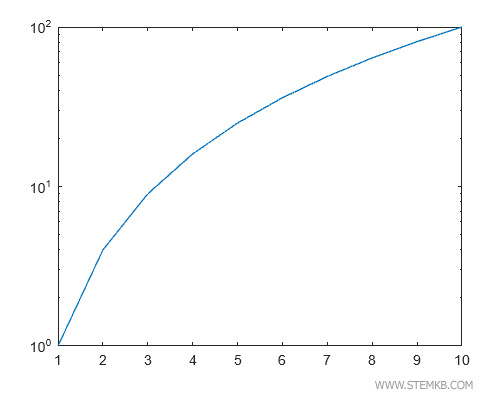
Aber das ist noch nicht alles! Wir wandeln dieses Diagramm nun in eine logarithmische Skala auf der y-Achse um. Dazu geben Sie einfach semilogy(x, y) ein und erleben, wie sich das Bild verändert.

>> semilogy(x,y)

In diesem modifizierten Diagramm ist die y-Achse logarithmisch skaliert, wodurch die Abstände zwischen 10⁰, 10¹ und 10² gleichmäßig werden.

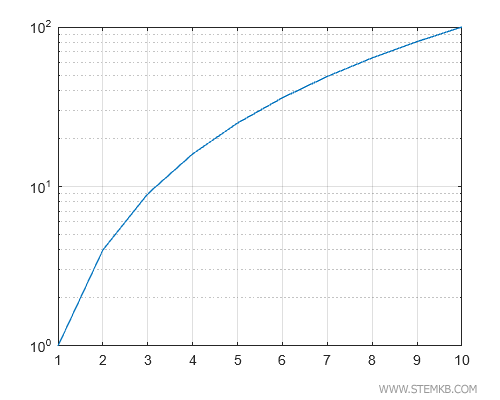
Um die Darstellung noch klarer zu gestalten, fügen wir Gitterlinien hinzu, indem wir grid on eingeben.

>> grid on

Jetzt ist die logarithmische Skala deutlich leichter zu lesen.

Was aber, wenn wir eine logarithmische Skala auch für die x-Achse benötigen? Kein Problem! Geben Sie einfach semilogx(x, y) ein.

>> semilogx(x,y)

Nun präsentiert sich das Diagramm mit einer logarithmischen Skala auf der x-Achse.

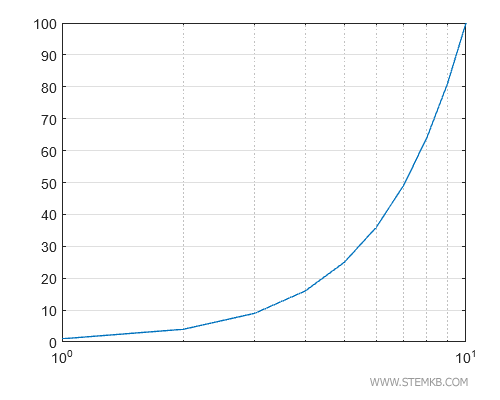
Doch damit nicht genug. Setzen wir beide Achsen auf eine logarithmische Skala, indem wir loglog (x, y) eingeben.

>> loglog(x,y)

Und voilà – ein Diagramm, bei dem beide Achsen logarithmisch skaliert sind.

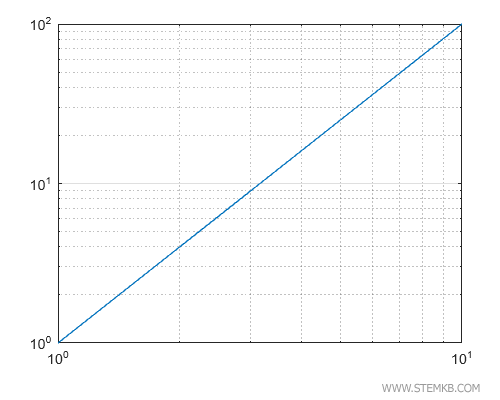
Zusammenfassend ermöglichen die Funktionen semilogx(), semilogy() und loglog() die Erstellung verschiedenster logarithmischer Diagramme in Matlab.