Erstellung von Polardiagrammen in Matlab

In dieser Lektion zeige ich Ihnen, wie man ein Polardiagramm in Matlab erstellt.

Was ist ein Polardiagramm? Polardiagramme sind diese faszinierenden kreisförmigen Darstellungen, die Daten anhand ihrer Polarkoordinaten visualisieren. Sie finden häufig Anwendung in wissenschaftlichen Bereichen und zeichnen sich durch ihre elegante Form aus.

Lassen Sie uns dies anhand eines anschaulichen Beispiels verdeutlichen.

Zunächst erstellen wir ein Array namens 'theta', welches unsere Winkelwerte aufnimmt:

>> theta = 0 : 0.1 : 2*pi;

Dieser Befehl generiert ein Array, das von 0 bis 2π (entspricht 360°) in 0.1er Schritten verläuft.

Anschließend definieren wir ein weiteres Array, 'y1', welches die Funktionswerte y1 für jede Winkelvariation in 'theta' umfasst:

>> y1=0.5+(1.3).^(theta);

Hierbei stellt 'y1' den Wertebereich unserer Funktion dar, während 'theta' den Definitionsbereich abdeckt.

Demnach enthalten die Arrays 'theta' und 'y1' die gleiche Anzahl von Elementen.

Jetzt, wo unsere Arrays vorbereitet sind, kommen wir zum aufregenden Teil: dem Erstellen des Polardiagramms. Geben Sie einfach den Befehl für die Polar()-Funktion ein:

 

>> PolarGraph = polar(theta,y1,"*");

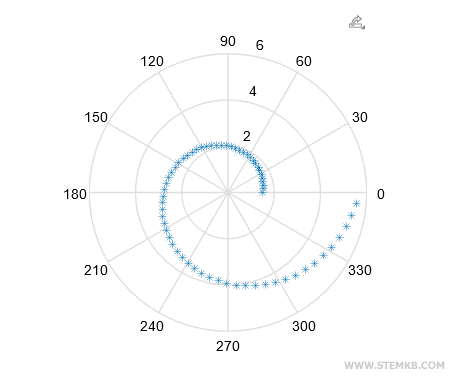
Voilà! Matlab wird nun auf elegante Weise das Verhalten der Funktion y1 mit ihren Polarkoordinaten abbilden.

In unserem Fall haben wir eine beeindruckende Spiral-Funktion kreiert.

Doch es gibt noch mehr zu entdecken! Wie wäre es, wenn wir zwei Funktionen in einem Polardiagramm darstellen?

Zuerst bereinigen wir die Anzeige mit 'clf', um ganz von vorne zu beginnen. Dann erstellen wir das 'theta'-Array erneut mit denselben Winkelwerten.

clf

Daraufhin erzeugen wir wieder das Array 'theta' mit den entsprechenden Winkelvariationen:

>> theta = 0 : 0.1 : 2*pi;

Nun definieren wir zwei neue Arrays, 'y1' und 'y2', für zwei unterschiedliche Funktionen, die sich mit 'theta' ändern:

>> y1=0.5+(1.3).^(theta);
>> y2 = 3*(1 - cos(theta));

Fassen wir die beiden Funktionen in einer Matrix [m] zusammen:

>> m = [y1;y2];

Zum Schluss verwenden wir die Polarplot()-Funktion, um das Polardiagramm zu erstellen:

>> PolarGraph = polarplot(theta,m);

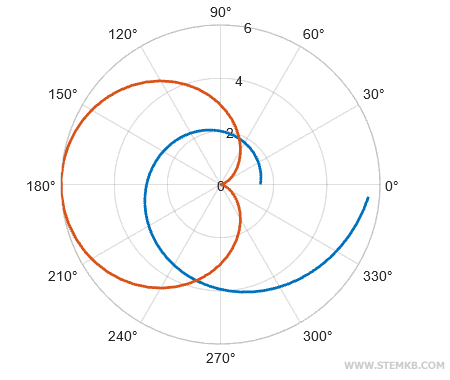
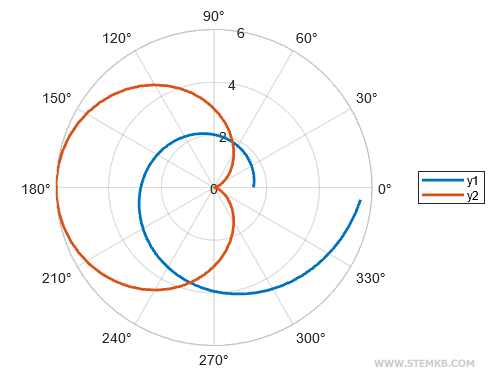
Beide Funktionen werden nun im Polardiagramm dargestellt.

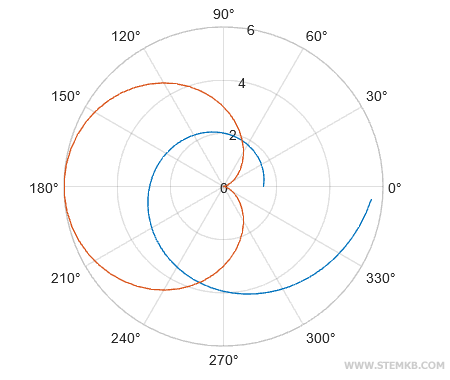
Um die Linienstärke zu erhöhen, können wir die set()-Funktion anwenden.

set(PolarGraph,"LineWidth",2);

So erreichen wir eine Verdoppelung der Linienstärke.

Zur weiteren Verfeinerung unseres Werkes fügen wir eine Legende mittels der legend()-Funktion hinzu.

legend("y1","y2");

Das Legendenfeld ergänzt nun ästhetisch den Rand unseres Diagramms.

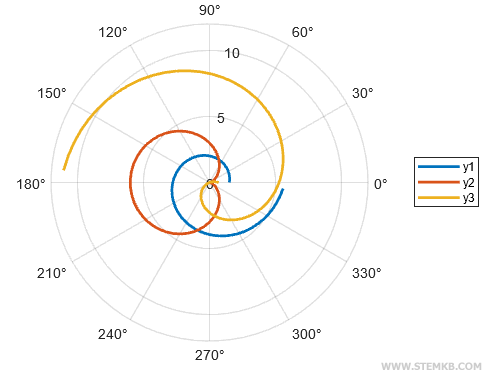
Beachten Sie, dass diese Technik nicht nur auf zwei Funktionen beschränkt ist. Sie können problemlos drei oder mehr Funktionen in einem Polardiagramm darstellen. Folgen Sie einfach dem gleichen Verfahren: Definieren Sie zusätzliche Funktionen, erstellen Sie eine Matrix mit allen Funktionen und nutzen Sie die polarplot(theta, m)-Funktion, um die sich überschneidenden Grafiken anzuzeigen. Das Ergebnis ist ein beeindruckendes Polardiagramm mit mehreren Funktionen, die um Ihre Aufmerksamkeit wetteifern. Beispielsweise könnten Sie eine weitere Funktion y3 = 0.7 - (1.9).*theta neben y1 und y2 definieren. Erstellen Sie dann eine Matrix mit drei Funktionen m = [y1; y2; y3]. Abschließend nutzen Sie die Funktion polarplot(theta, m), um die drei sich überlagernden Graphen im selben Polardiagramm zu präsentieren. Das Polardiagramm zeigt nun drei überlappende Funktionen.

Jetzt zeigt das Polardiagramm drei Funktionen.