Erstellung von Treppenstufen-Diagrammen in Matlab

Heute widmen wir uns in Matlab den Treppenstufen-Diagrammen und entdecken, wie lehrreich und interessant sie sein können.

Was macht diese Treppenstufen-Diagramme so besonders? Stellen Sie sich das Schaubild einer Funktion vor, jedoch nicht als durchgängige, glatte Kurve, sondern in Form von Treppenstufen. Diese Diagramme eignen sich ausgezeichnet, um zu veranschaulichen, wie sich die Werte einer Funktion in deutlich abgrenzbaren Schritten erhöhen oder verringern.

Beginnen wir mit einem einfachen Beispiel.

Nehmen wir an, wir haben ein Array 'x', das Werte von 1 bis 20 enthält.

>> x=linspace(1,20,20);

Dieses Array 'x' bildet den Definitionsbereich unserer Funktion.

Als Nächstes generieren wir ein Array 'y', welches die Funktionswerte von y=f(x) repräsentiert.

>> y=x

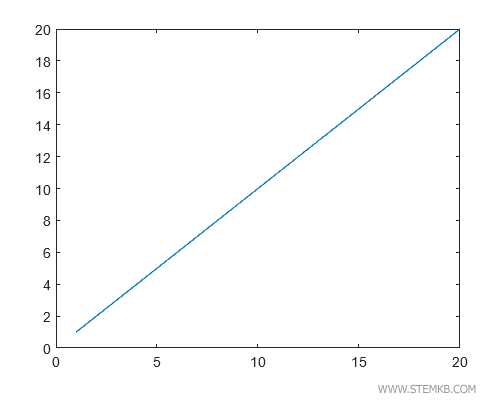
Geben wir nun plot(x,y) ein, erhalten wir das Schaubild von y=f(x).

>> plot(x,y)

Zu sehen ist eine kontinuierliche Linie, die sich von 1 bis 20 erstreckt. In unserem Fall handelt es sich um eine Gerade, die durch den Ursprung verläuft.

Lassen Sie uns jedoch eine interessantere Wendung hinzufügen. Mit dem Befehl stairs(x,y) erstellen wir ein Treppenstufen-Diagramm.

>> stairs(x,y)

Durch die Funktion stairs(x,y) verknüpfen wir benachbarte Punkte mit Stufen statt einer durchgehenden Linie.

Das Ergebnis ist ein beeindruckendes Treppenstufen-Diagramm.

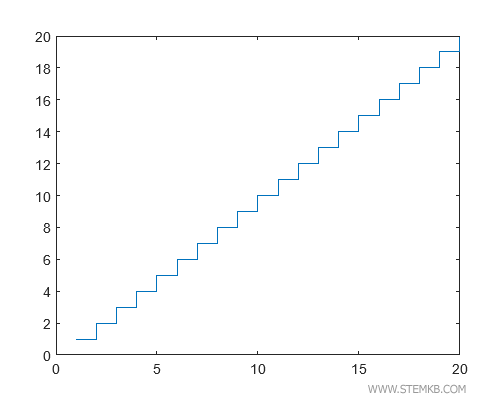
In diesem Fall sind alle Stufen gleich hoch, da die lineare Funktion an jedem Punkt gleichmäßig steigt.

Kommen wir nun zu einem noch faszinierenderen Beispiel.

Wir definieren eine Funktion y=x², die für jeden x-Wert dessen Quadrat berechnet.

y=x.^2

Der kontinuierliche Graph dieser Funktion zeigt eine exponentielle Kurve.

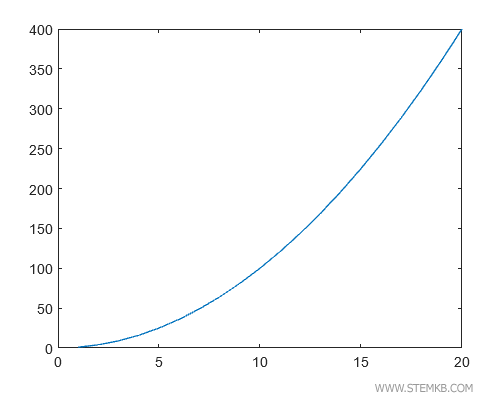
Verwenden wir jedoch stairs(x,y) für das Treppenstufen-Diagramm...

>> stairs(x,y)

...ergibt sich ein Graph mit Stufen unterschiedlicher Höhe, die dort am höchsten sind, wo die Funktion am stärksten zunimmt.

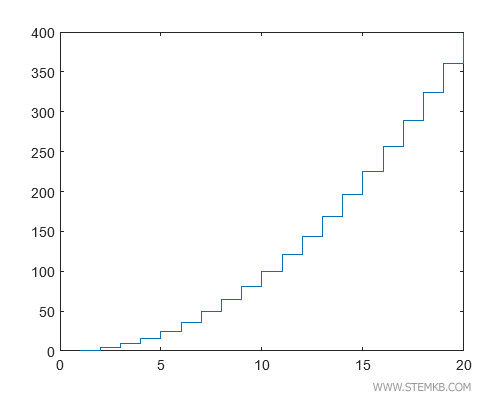
Hier steigen die Stufenhöhen mit zunehmendem x-Wert an, was auf ein überproportionales Wachstum der Funktion hindeutet.

Wie stellt man mehrere Graphen in einem einzigen Diagramm dar?

Vielleicht fragen Sie sich: "Wie kann ich zwei Funktionen im selben Diagramm vergleichen?" Das ist problemlos möglich!

Erstellen wir zum Beispiel ein Array Y mit zwei Elementen.

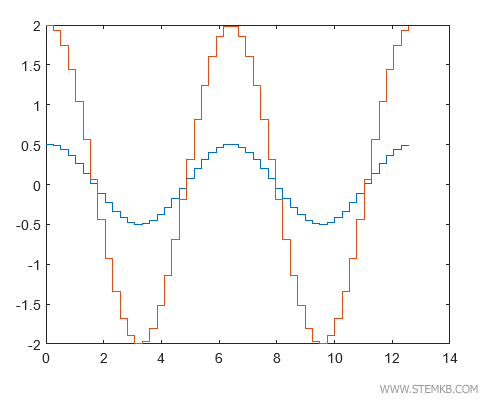
Wir verwenden 0,5cos(X) als erstes und 2cos(X) als zweites Element.

>> X = linspace(0,4*pi,50)';
>> Y = [0.5*cos(X), 2*cos(X)];

Mit stairs(Y) oder stairs(X,Y) können wir beide Treppenstufen-Graphen gemeinsam darstellen.

>> stairs(X,Y)

Voilà! So erhalten wir ein einziges kartesisches Diagramm, das die Treppenstufen-Diagramme beider Funktionen zeigt und ihren Vergleich erleichtert.

Und für die Ambitionierten unter Ihnen: Sie können sogar drei oder mehr Funktionen im selben Diagramm darstellen! Definieren Sie einfach ein Array mit drei oder mehr Elementen und folgen Sie dem gleichen Verfahren.