Symbolische Variablen in Matlab

Heute möchte ich Sie in die Welt der symbolischen Variablen in Matlab einführen.

Was genau versteht man unter einer symbolischen Variable? Es handelt sich dabei um eine spezielle Art von Variable, die lediglich Symbole wie beispielsweise "x" speichert und nicht etwa konkrete Zahlenwerte. Dies eröffnet die Möglichkeit, symbolische algebraische Berechnungen mit einer oder mehreren Unbekannten durchzuführen. Denken Sie hierbei an das Lösen von Gleichungen mit mehreren Variablen oder das Addieren von Polynomen.

Die Definition einer symbolischen Variable erfolgt über die syms Funktion.

Als Beispiel können Sie die Variable "x" folgendermaßen definieren:

>> syms x

Sie möchten mehrere solcher Variablen gleichzeitig deklarieren? Kein Problem, trennen Sie diese einfach durch Leerzeichen:

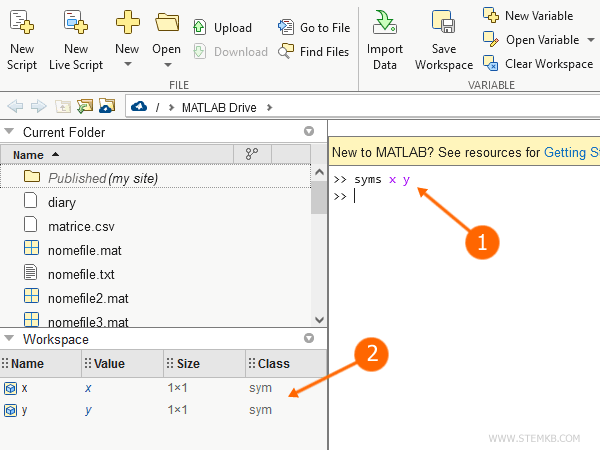
>> syms x y

Nach jeder Deklaration erscheint die symbolische Variable sichtbar im Matlab-Arbeitsbereich.

Interessanterweise gehören diese symbolischen Variablen zur "sym" Klasse.

Nehmen wir an, wir haben zwei Polynome:

$$ P(x) = 2x + y $$

$$ Q(x) = 4x - 2y $$

Das Ziel ist, diese beiden zu multiplizieren:

$$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$

Für solche algebraischen Operationen in Matlab definieren Sie zunächst die symbolischen Variablen "x" und "y" mittels:

>> syms x y

Geben Sie anschließend den Ausdruck pq = (2x+y)(4x-2y) in die Befehlszeile ein:

>> pq = (2*x+y)*(4*x-2*y)

ans =
(4*x - 2*y)*(2*x + y)

Matlab identifiziert "x" und "y" als Symbole und gibt uns daraufhin den symbolischen Ausdruck zurück.

Hierbei ist anzumerken, dass Matlab die Variablen "x" und "y" nicht durch Zahlen ersetzt, sondern sie als reine Symbole behandelt.

Um das Resultat der algebraischen Operation zu erhalten, nutzen Sie die Funktion expand(pq):

>> expand(pq)

ans =
8*x^2 - 2*y^2

Matlab führt die typische symbolische Algebra-Berechnung aus und gibt das Produkt der beiden Polynome zurück.

Das Ergebnis lautet: 8x²-2y²

Als Abschluss überprüfen wir das Resultat noch manuell. Eine manuelle Multiplikation der Polynome zeigt: $$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$ $$ P(x) \cdot Q(x) =2x \cdot 4x + 2x \cdot (-2y) + y \cdot 4x + y \cdot (-2y) $$ $$ P(x) \cdot Q(x) =8x^2 - 4xy + 4xy -2y^2 $$ $$ P(x) \cdot Q(x) =8x^2 -2y^2 $$ Wie Sie erkennen, stimmt das Resultat überein. Das war eine kurze Einführung zum Thema für heute.