Bestimmte integrale in Matlab

In dieser Anleitung erläutere ich Ihnen Schritt für Schritt, wie man das bestimmte Integral einer mathematischen Funktion mit Matlab berechnet.

Was genau versteht man unter einem bestimmten Integral? Es dient dazu, den zwischen einer Funktion f(x) – dem sogenannten Integranden – und der horizontalen x-Achse innerhalb eines festgelegten Intervalls [a, b] liegenden Flächeninhalt zu bestimmen. Mathematisch ausgedrückt sieht das so aus: $$ \int_a^b f(x) \ dx $$

In Matlab stehen Ihnen zwei Funktionen zur Verfügung, um solche Integrale zu lösen: int() und quad().

Die int() Funktion

Um das Integral einer Funktion zu berechnen, nutzen Sie int() in Matlab wie folgt:

int(Funktion, a, b)

Die Funktion benötigt drei Parameter:

• Der mathematische Ausdruck der Funktion f(x)
• Die untere Integrationsgrenze (a)
• Die obere Integrationsgrenze (b)

Ein wichtiger Hinweis: int() basiert auf symbolischer Berechnung. Bevor Sie also den Ausdruck der zu integrierenden Funktion eingeben, sollten Sie die unbekannte Variable mit der syms-Funktion als Symbol festlegen.

Ein praktisches Beispiel:

Betrachten Sie das einfache Integral

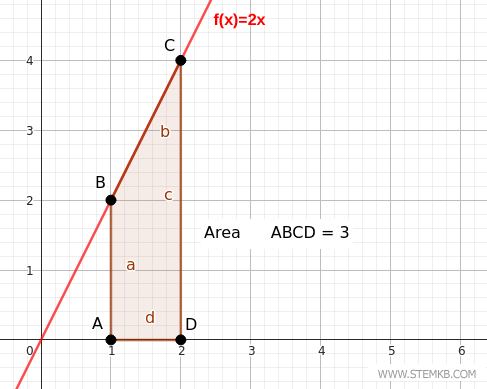
$$ \int_1^2 2x \ dx $$

und das Integrationsintervall liegt zwischen 1 und 2.

Zunächst definieren Sie das Symbol für die Variable x:

syms x

Daraufhin geben Sie den int() Befehl ein und setzen 2*x als ersten Parameter, gefolgt von den Grenzen 1 und 2.

int(2*x,1,2)

Das Ergebnis, das Matlab Ihnen liefert, ist das bestimmte Integral von 2x über das Intervall [1,2], welches 3 beträgt.

ans = 3

Das bestimmte Integral von 2x über [1,2] ist leicht nachzuvollziehen. Die Stammfunktion von f(x) = 2x ist F(x) = x². Die Berechnung ergibt $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$

Die quad() Funktion

Jetzt zur quad() Funktion.

Um Integrale zu berechnen, kann man in Matlab auch quad() verwenden. Der Aufruf erfolgt ähnlich:

quad(Funktion, a, b)

Wiederholen wir das oben beschriebene Beispiel:

$$ \int_1^2 2x \ dx $$

Hier definieren Sie eine anonyme Funktion:

>> f = @(x) 2*x

Dann verwenden Sie quad(f,1,2), um das bestimmte Integral zu berechnen. Das Ergebnis ist erneut 3.

>> quad(f,1,2)

ans=3

Interessanterweise liefert uns die quad() Funktion dasselbe Ergebnis wie die int() Funktion.

Doch was unterscheidet diese beiden Funktionen?

In Matlab dienen sowohl int() als auch quad() zur Berechnung bestimmter Integrale. Allerdings basieren sie auf unterschiedlichen Methoden:

• int() löst Integrale mithilfe von numerischen Verfahren, wie z.B. der Trapezregel.
• quad() setzt auf ein adaptives Quadraturverfahren basierend auf dem Gauss-Kronrod-Algorithmus, welches oft effizienter ist.

Abschließend: Mit Matlab besitzen Sie ein mächtiges Werkzeug zur Integralberechnung – unerlässlich für Ingenieure, Physiker und Mathematiker. Mit etwas Übung werden Sie bald in der Lage sein, komplexe Integrale spielend leicht zu lösen.