Grenzwert einer Funktion mit Matlab
Heute wollen wir in die faszinierende Welt der Funktionsgrenzwerte eintauchen und dabei die rechnerischen Fähigkeiten von Matlab nutzen. Wir werden nicht nur das Konzept verstehen, sondern es auch anhand von anschaulichen Beispielen in die Praxis umsetzen.
Bevor wir beginnen, klären wir kurz, was Funktionsgrenzwerte überhaupt sind. Ein Funktionsgrenzwert ist der Wert, den eine Funktion schrittweise annimmt, wenn ihre unabhängige Variable sich einem bestimmten Punkt nähert. Laienhaft ausgedrückt zeigt es das Verhalten der Funktion in der Nähe dieses spezifischen Punktes.
Starten Sie das Verfahren, indem Sie 'x', die unabhängige Variable, in die Matlab-Befehlszeile mit dem 'syms'-Befehl eingeben.
syms x
Um den Ball ins Rollen zu bringen, beschäftigen wir uns mit der Funktion f(x) = (x+1)/(x-1), wobei 'x' unsere unabhängige Variable ist. Wir wollen den Grenzwert finden, wenn 'x' gegen Unendlich strebt.
$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$
Geben Sie dann den Befehl 'limit()' ein. Setzen Sie die Funktion f(x) als ersten Parameter, 'x' als zweiten und 'Inf' (was positive Unendlichkeit bedeutet) als dritten Parameter. Drücken Sie dann einfach Enter.
limit((x+1)/(x-1),x,Inf)
Voilà! Matlab tritt in Aktion und gibt treu den Grenzwert der Funktion zurück.
ans = (sym) 1
Und siehe da, der Grenzwert der Funktion, wenn 'x' gegen Unendlich strebt, beträgt eins.
Nehmen Sie nicht einfach mein Wort dafür. Wie wir sehen können, beträgt der Grenzwert der Funktion f(x) = (x+1)/(x-1), wenn 'x' gegen Unendlich strebt, tatsächlich eins. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$ Der Grenzwert unserer Funktion beträgt eins, wenn 'x' sich in Richtung Unendlichkeit bewegt.
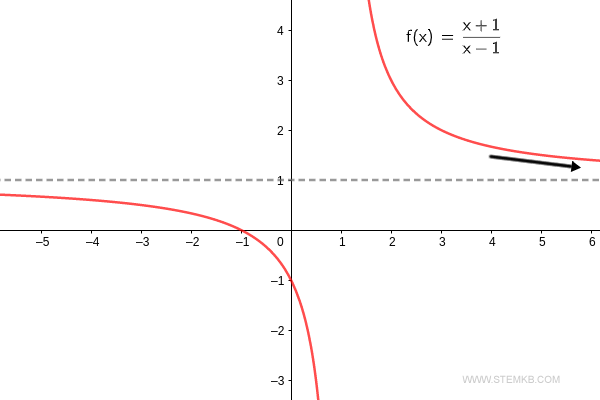
Wenn Sie neugierig auf den Grenzwert bei x→-∞ sind, fügen Sie einfach '-inf' als dritten Parameter zum Befehl hinzu.
limit((x+1)/(x-1),x,-inf)
Wenn 'x' stürmisch gegen negative Unendlichkeit geht, steigt die Funktion in die entgegengesetzte Richtung und nähert sich eins.
ans = (sym) 1
Um den Punkt zu beweisen: Der Grenzwert der Funktion f(x) = (x+1)/(x-1) für x→-∞ ist fest eins. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$ Man kann sich den Graphen der Funktion ansehen, wie er sich in Richtung negative Unendlichkeit verläuft.
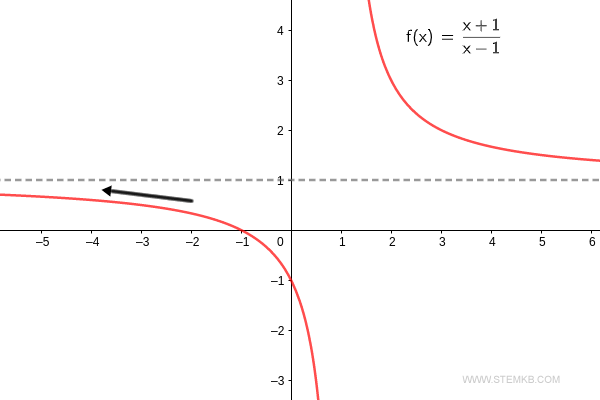
Möchten Sie den Grenzwert einer Funktion an einem spezifischen Punkt 'x0' ermitteln, so geben Sie diesen Punkt schlichtweg als dritten Parameter ein.
Angenommen, wir sind daran interessiert, den Grenzwert der Funktion zu bestimmen, wenn 'x' gegen die Zahl zwei konvergiert.
limit((x+1)/(x-1),x,2)
Hier ergibt sich ein Grenzwert von drei.
ans = (sym) 3
Bei näherer Untersuchung zeigt sich, dass der Grenzwert der Funktion f(x)=(x+1)/(x-1) bei einer Annäherung von 'x' an die Zahl 2 tatsächlich drei beträgt: $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$ Der Grenzwert der Funktion liegt also bei 3, wenn 'x' sich der Zahl 2 nähert.
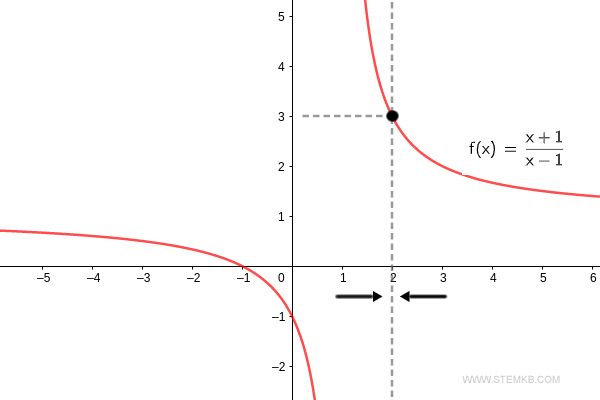
Wenn Sie nur an dem rechtsseitigen Grenzwert interessiert sind, fügen Sie 'right' als vierten Argument im selben Befehl hinzu.
limit((x+1)/(x-1),x,1,'right')
Das Ergebnis? Der rechtsseitige Grenzwert der Funktion, wenn 'x' sich der 1 nähert, ist positive Unendlichkeit ( ∞ ).
ans = (sym) ∞
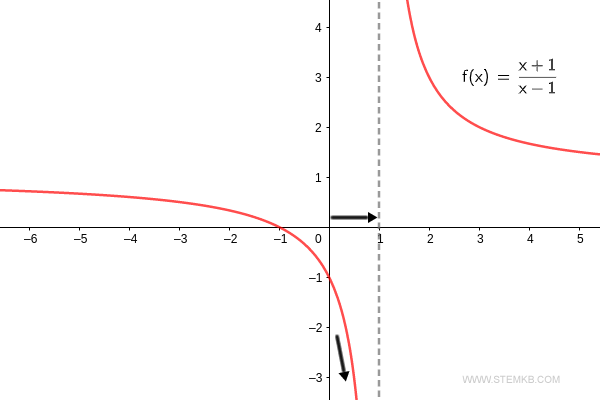
Zur Bestätigung: Wenn sich die Funktion f(x) = (x+1)/(x-1) von rechts der Stelle x=1 nähert, steigt sie in Richtung positive Unendlichkeit. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$ Also strebt der rechtsseitige Grenzwert der Funktion gegen Unendlichkeit, wenn 'x' sich der Zahl 1 nähert.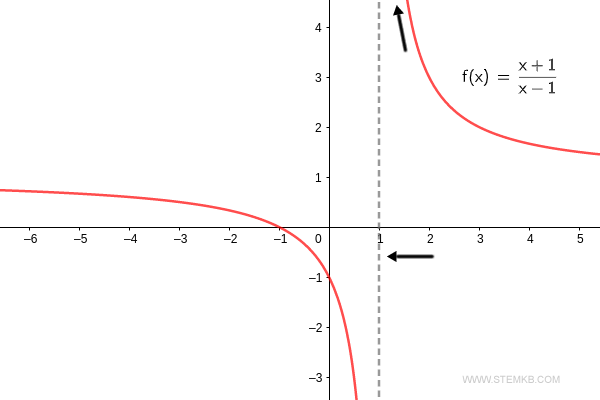
Wenn Sie dagegen den linksseitigen Grenzwert bestimmen möchten, fügen Sie einfach 'left' als vierten Parameter hinzu.
limit((x+1)/(x-1),x,1,'left')
Und was ergibt sich? Der linksseitige Grenzwert der Funktion, wenn 'x' sich der 1 nähert, ist negative Unendlichkeit (-∞).
ans = (sym) -∞
Bei der Überprüfung stellen wir fest, dass der linksseitige Grenzwert der Funktion f(x) = (x+1)/(x-1), wenn x→1- strebt, tatsächlich gegen negative Unendlichkeit geht. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$ Somit fällt der linksseitige Grenzwert der Funktion gegen negative Unendlichkeit, wenn 'x' sich der Zahl 1 nähert.
Damit sind Sie nun bestens vertraut, wie Sie Matlab zur Berechnung von Funktionsgrenzwerten nutzen können.