Diagonalen einer Matrix in Matlab extrahieren
In dieser Lektion erkläre ich Ihnen, wie Sie die Diagonalelemente einer Matrix in Matlab herausfiltern können.
Was versteht man unter der Diagonale einer Matrix? Die Hauptdiagonale einer Matrix besteht aus den Elementen, die sich entlang der von links oben nach rechts unten verlaufenden Diagonale befinden. Betrachten Sie zum Beispiel die Hauptdiagonale in der folgenden Matrix, in der die Elemente 1, 5, 9 in Rot hervorgehoben sind. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
Sehen wir uns ein praktisches Beispiel an.
Erstellen Sie eine quadratische 3x3-Matrix mit jeweils drei Zeilen und Spalten, die folgende Elemente enthält.
>> M=[1 2 3; 4 5 6; 7 8 9]
M =
1 2 3
4 5 6
7 8 9
Verwenden Sie nun die Funktion diag(M), um die Elemente auf der Hauptdiagonale der Matrix zu isolieren.
>> diag(M)
ans =
1
5
9
Diese Funktion extrahiert die Elemente der Hauptdiagonale der Matrix.
In diesem Fall sind das die Werte 1, 5 und 9.
$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
Mit der diag()-Funktion können Sie auch andere Diagonalen der Matrix extrahieren.
Um beispielsweise die Elemente der Diagonale über der Hauptdiagonale zu erhalten, geben Sie diag(M,1) ein.
>> diag(M,1)
ans =
2
6
Hier extrahiert diag(M,1) die Zahlen 2 und 6, die sich auf der darüberliegenden Diagonale befinden.
$$ M = \begin{pmatrix} 1 & \color{red}2 & 3 \\ 4 & 5 & \color{red}6 \\ 7 & 8 & 9 \end{pmatrix} $$
Geben Sie nun diag(M,2) ein, um die Elemente der darüber hinausgehenden Diagonale zu extrahieren.
>> diag(M,2)
ans = 3
Mit diesem Befehl werden die Elemente einer weiteren Diagonalebene extrahiert... und so weiter.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$
Um Diagonalen unterhalb der Hauptdiagonale zu extrahieren, verwenden Sie einen negativen Wert als zweiten Parameter.
Um beispielsweise die Elemente der Diagonale unter der Hauptdiagonale zu erhalten, geben Sie diag(M,-1) ein.
>> diag(M,-1)
ans =
4
8
Mit diag(M,-1) werden die Elemente unterhalb der Hauptdiagonale isoliert.
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ \color{red}4 & 5 & 6 \\ 7 & \color{red}8 & 9 \end{pmatrix} $$
Um alle anderen Matrixelemente zu entfernen und nur jene der Hauptdiagonale zu behalten, verwenden Sie diag(diag(M)).
>> diag(diag(M))
ans =
Diagonalmatrix
1 0 0
0 5 0
0 0 9
Dadurch erhalten Sie eine Diagonalmatrix.
$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \end{pmatrix} $$
Wie extrahiert man die Sekundärdiagonale?
Die Sekundärdiagonale, oder Antidiagonale, besteht aus den Matrixelementen, die von rechts nach links verlaufend, vom letzten Element in der oberen rechten Ecke ausgehen.
In der 3x3-Matrix unseres Beispiels setzt sich die Sekundärdiagonale aus den Elementen 3, 5, 7 zusammen.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$
Um die Sekundärdiagonale zu extrahieren, spiegeln Sie die Matrix horizontal mit der Funktion fliplr().
Verwenden Sie hierfür den Befehl diag(fliplr(M)).
>> diag(fliplr(M))
ans =
3
5
7
Mit diag(fliplr(M)) werden die Elemente der Sekundärdiagonale isoliert.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$
Hinweis: Sie können auch den zweiten Parameter der Funktion nutzen, um Diagonalen oberhalb oder unterhalb der Hauptdiagonale zu extrahieren. Um die darüberliegenden Diagonalen zu erhalten, geben Sie einen positiven Wert ein. So extrahiert beispielsweise diag(fliplr(M),1) die Elemente 2 und 4, die sich unmittelbar über der Hauptdiagonale befinden. $$ M = \begin{pmatrix} 1 & \color{red}2 & \color{green}3 \\ \color{red}4 & \color{green}5 & 6 \\ \color{green}7 & 8 & 9 \end{pmatrix} $$ Um die darunterliegenden Diagonalen zu extrahieren, verwenden Sie einen negativen Wert. Zum Beispiel isoliert diag(fliplr(M),-1) die Elemente 6 und 8, die sich unmittelbar unter der Hauptdiagonale befinden.
$$ M = \begin{pmatrix} 1 & 2 & \color{green}3 \\ 4 & \color{green}5 & \color{red}6 \\ \color{green}7 & \color{red}8 & 9 \end{pmatrix} $$ .
Die diag()-Funktion erlaubt es Ihnen, Elemente entlang der Diagonalen auch aus rechteckigen Matrizen zu extrahieren.
Als Beispiel können Sie eine rechteckige Matrix mit 3 Zeilen und 4 Spalten erstellen.
>> M2=[1 1 1 1 ; 2 2 2 2 ; 3 3 3 3]
M2 =
1 1 1 1
2 2 2 2
3 3 3 3
Verwenden Sie dann den Befehl diag(M2), um fortzufahren.
>> diag(M2)
ans =
1
2
3
Mit dem Befehl diag(M2) werden die Elemente entlang der Diagonale extrahiert, beginnend mit dem Element in der oberen linken Ecke.
$$ M = \begin{pmatrix} \color{red}1 & 1 & 1 & 1 \\ 2 & \color{red}2 & 2 & 2 \\ 3 & 3 & \color{red}3 & 3 \end{pmatrix} $$
So können Sie jede beliebige Diagonale extrahieren, unabhängig davon, ob es sich um eine Quadratmatrix handelt oder nicht.
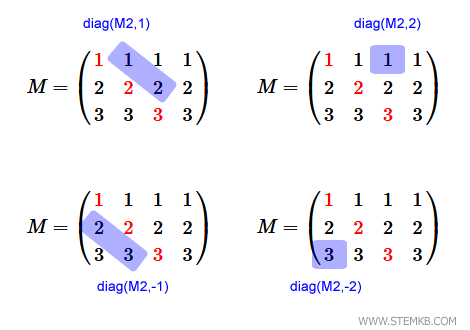
Anmerkung: Auch bei rechteckigen Matrizen lassen sich die Diagonalen oberhalb oder unterhalb der Hauptdiagonalen extrahieren. Dies geschieht durch Angabe einer positiven oder negativen ganzen Zahl als zweiten Parameter. Zum Beispiel können Sie diag(M2,1) oder diag(M2,-1) für die Diagonalen ober- bzw. unterhalb der Hauptdiagonale verwenden. Ähnlich verhält es sich mit diag(M2,2) oder diag(M2,-2) für die weiteren Diagonalen.
Um die sekundären Diagonalen einer rechteckigen Matrix zu extrahieren, müssen Sie diese von rechts nach links umdrehen. Zum Extrahieren der sekundären Diagonale nutzen Sie diag(fliplr(M2)). Hierbei startet die sekundäre Diagonale vom obersten rechten Element der rechteckigen Matrix. $$ M = \begin{pmatrix} 1 & 1 & 1 & \color{red}1 \\ 2 & 2 & \color{red}2 & 2 \\ 3 & \color{red}3 & 3 & 3 \end{pmatrix} $$