Ersetzung von Diagonalen in einer Matlab-Matrix

In dieser Lektion zeige ich Ihnen, wie Sie die Elemente entlang der Diagonalen einer Matrix in Matlab austauschen können.

Was versteht man unter den Diagonalen einer Matrix? Es handelt sich um jene Elemente, die sich entlang der Diagonalen von der oberen rechten Ecke zur unteren linken Ecke oder umgekehrt erstrecken. Beispielsweise setzt sich die Hauptdiagonale der Matrix M aus den Elementen 1, 5, 9 zusammen. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Lassen Sie uns dies an einem einfachen praktischen Beispiel illustrieren.

Erstellen wir zunächst eine 3x3 Quadratmatrix mit jeweils drei Zeilen und Spalten:

>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

Die Hauptdiagonale dieser Matrix besteht aus den Elementen 1, 5, 9.

$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Geben Sie den Befehl spdiags([-1;-5;-9],0,M) in Matlab ein, um die Elemente der Hauptdiagonale durch -1, -5, -9 zu ersetzen.

>> spdiags([-1;-5;-9],0,M)
ans =
-1 2 3
4 -5 6
7 8 -9

• Der erste Parameter des Befehls ist der Spaltenvektor [-1;-5;-9], der die neuen Diagonalelemente enthält.
• Der zweite Parameter, 0, bezeichnet den Index der Diagonale, auf der die Elemente ersetzt werden sollen. Die Hauptdiagonale hat hierbei den Index 0.

  Hinweis: Index 1 bezieht sich auf die Diagonale oberhalb der Hauptdiagonale, während Index -1 die unterhalb der Hauptdiagonale bezeichnet. Entsprechend sind die Indizes 2 und -2 für die weiteren Diagonalen darüber und darunter.

• Der dritte Parameter, M, ist der Name der Variablen, in der die Matrix gespeichert ist.

Mit diesem Befehl wird die Matrix so modifiziert, dass die neuen Elemente in die Hauptdiagonale eingefügt werden.

$$ M = \begin{pmatrix} \color{red}{-1} & 2 & 3 \\ 4 & \color{red}{-5} & 6 \\ 7 & 8 & \color{red}{-9} \end{pmatrix} $$

Um nun die Elemente der darüber liegenden Diagonale zu ändern, verwenden Sie den Befehl spdiags([-1;-5;-9],1,M).

>> spdiags([-1;-5;-9],1,M)
ans =
1 -5 3
4 5 -9
7 8 9

Diese Anweisung ersetzt die Elemente der Diagonale oberhalb der Hauptdiagonale.

$$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ 4 & 5 & \color{red}{-9} \\ 7 & 8 & 9 \end{pmatrix} $$

Anmerkung: Das erste Element -1 des Vektors [-1;-5;-9] wird nicht in die Matrix aufgenommen, da es außerhalb liegt. Daher erscheinen nur -5 und -9 in der Matrix.

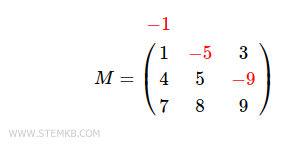
Und wie ersetzt man Elemente der Nebendiagonale?

Die Nebendiagonale beginnt oben rechts und endet unten links.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{3} \\ 4 & \color{red}{5} & 6 \\ \color{red}{7} & 8 & 9 \end{pmatrix} $$

Um Elemente auf der Nebendiagonale zu ersetzen, nutzen Sie die Funktionen spdiags() und fliplr().

>> fliplr(spdiags([-1;-5;-9],0,fliplr(M)))
ans =
1 2 -1
4 -5 6
-9 8 9

Die Funktion fliplr() spiegelt die Matrix horizontal.

$$ \text{ fliplr }(M) = \begin{pmatrix} 3 & 2 & 1 \\ 6 & 5 & 4 \\ 9 & 8 & 7 \end{pmatrix} $$

Anschließend ersetzt spdiags() die Werte in der Hauptdiagonale dieser gespiegelten Matrix.

$$ \text{ fliplr }(M) = \begin{pmatrix} \color{red}{-1} & 2 & 1 \\ 6 & \color{red}{-5} & 4 \\ 9 & 8 & \color{red}{-9} \end{pmatrix} $$

So werden in der ursprünglichen Matrix M die Elemente der Nebendiagonale ausgetauscht.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{-1} \\ 4 & \color{red}{-5} & 6 \\ \color{red}{-9} & 8 & 9 \end{pmatrix} $$

Mit dieser Methode können Sie ebenfalls die Werte auf den anderen Diagonalen der Matrix anpassen.

Hinweis: Um die Diagonalen über oder unter der Nebendiagonale zu modifizieren, ändern Sie den Index in der spdiags()-Funktion auf 1 oder -1. Zum Beispiel, um die Elemente über der Nebendiagonale zu ändern, nutzen Sie den Befehl
fliplr(spdiags([-1;-5;-9],1,fliplr(M))) $$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ \color{red}{-9} & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$ Umgekehrt, um die Elemente unterhalb der Nebendiagonale zu ändern, verwenden Sie den Befehl
fliplr(spdiags([-1;-5;-9],-1,fliplr(M))) $$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & \color{red}{-1} \\ 7 & \color{red}{-5} & 9 \end{pmatrix} $$