Lineare Gleichungssysteme in Matlab

In dieser Matlab-Einheit erkläre ich Ihnen, wie Sie ein lineares Gleichungssystem mithilfe von Matrix- und Vektoroperationen lösen können.

Beginnen wir mit einem anschaulichen Beispiel.

Unser lineares Gleichungssystem besteht hier aus zwei Unbekannten in zwei Gleichungen.

$$ \begin{cases} x+5y-3 = 0 \\ \\ 2x-4y+8=0 \end{cases} $$

Hinweis: Eine Gleichung wird als linear bezeichnet, wenn der höchste Grad der Unbekannten eins ist.

Bringen wir das Gleichungssystem zunächst in die Normalform ax+by=c.

Indem wir die konstanten Terme auf die rechte Seite verlagern, belassen wir die Unbekannten und deren Koeffizienten auf der linken Seite.

$$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$

Nun wandeln wir das Gleichungssystem in die Vektorform um.

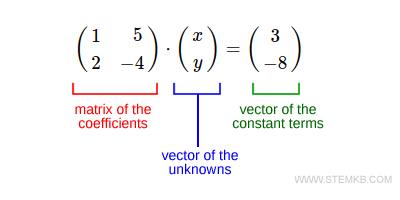
$$ \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$

Die Matrix auf der linken Seite ist die Koeffizientenmatrix für die Variablen x und y.

$$ A = \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} $$

Der erste Vektor stellt den Vektor der Unbekannten dar.

$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} $$

Der letzte Vektor beinhaltet die konstanten Terme der beiden Gleichungen.

$$ \vec{b} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$

Lassen Sie uns nun betrachten, wie wir diese Informationen in die Matlab-Arbeitsumgebung überführen.

Zur Definition der Koeffizientenmatrix in Matlab erstellen Sie ein zweidimensionales Array.

Geben Sie A = [1, 5; 2, -4] in der Befehlszeile ein.

>> A = [ 1 , 5 ; 2 , -4 ]
A =
1 5
2 -4

Für den Vektor der konstanten Terme in Matlab erstellen Sie ein eindimensionales Array.

Tippen Sie b = [3; -8] ein.

>> b = [ 3 ; -8 ]
b =
3
-8

In Vektorform stellt das Gleichungssystem das Produkt einer Matrix mit einem Vektor dar.

$$ A \cdot \vec{x} = \vec{b} $$

Um die Lösungen des Systems zu ermitteln, isolieren wir den Vektor x, indem wir alles andere auf die rechte Seite bringen.

$$ \vec{x} = A^{-1} \cdot \vec{b} $$

Hierbei ist A^-1 die Inverse der Koeffizientenmatrix A des Gleichungssystems.

Berechnen Sie nun A^-1 mal b in Matlab, indem Sie inv(A)*b eingeben.

>> inv(A)*b
ans =
-2
1

Das Ergebnis sind die Werte von x und y des Unbekanntenvektors.

$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \end{pmatrix} $$

Mit diesem Ansatz haben Sie die Lösung des Gleichungssystems gefunden.

$$ x=-2 $$

$$ y=1 $$

Das lineare Gleichungssystem hat somit die Lösung (x;y)=(-2;1).

Zur Überprüfung der Korrektheit der Lösung: Setzen Sie die Werte x=-2 und y=1 in das ursprüngliche Gleichungssystem ein und führen Sie die algebraischen Berechnungen durch. $$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$ $$ \begin{cases} -2 + 5 \cdot 1 =3 \\ \\ 2 \cdot (-2) -4 \cdot 1 =-8 \end{cases} $$ $$ \begin{cases} 3 =3 \\ \\ -8 =-8 \end{cases} $$ Da alle Gleichungen erfüllt sind, ist die Lösung x=-2 und y=1 korrekt.