Dünne Matrizen in Matlab

In dieser Online-Lektion erkläre ich, wie man dünne Matrizen mit Matlab erstellt.

Was ist eine dünne Matrix? Dünne Matrizen ermöglichen es, sehr große Matrizen zu erzeugen, während weniger Computerspeicher belegt wird. Wenn Sie beispielsweise eine Matrix mit vielen konstanten Werten (z.B. Null) erstellen, wiederholen Sie dieselben Werte in mehreren Elementen und belegen unnötigerweise einen großen Teil des Speichers. $$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ Um die Menge des belegten Speichers zu reduzieren, können Sie dieselbe Matrix als dünne Matrix erzeugen, bei der die Daten komprimiert werden, da Nullwerte ignoriert werden.

In Matlab können Sie dünne Matrizen verwenden, um komprimierte Einheits- und Diagonalmatrizen zu erstellen.

Dünne Einheitsmatrix

Lassen Sie mich Ihnen ein praktisches Beispiel geben.

Erstellen Sie eine Einheitsmatrix mit der Funktion eye(4)

>> eye(4)
ans =
Diagonalmatrix
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

In der Matrix gibt es 12 Nullen und 4 Einsen. Also wird der größte Teil des Raums in der Matrix (12 von 16 Elementen) unnötigerweise durch Nullen belegt.

Erstellen Sie jetzt dieselbe Einheitsmatrix mit der Technik der dünnen Matrizen durch den Befehl speye(4).

>> speye(4)
ans =
Komprimierte Spaltendünne Matrix (Zeilen = 4, Spalten = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

In der dünnen Matlab-Matrix werden nur die Positionen (Zeile, Spalte) der Matrix aufgelistet, an denen es Nicht-Null-Werte gibt, wodurch weniger Speicherplatz belegt wird.

Aus diesem Grund wird sie "dünne" Matrix genannt.

Beachten Sie, dass die dünne Matrix weniger Speicher belegt, weil sie nur die nützlichen Informationen berücksichtigt. In einer Einheitsmatrix sind Nullen unbedeutende Elemente in der Matrixberechnung, daher werden sie entfernt. Dies reduziert den belegten Platz im Speicher (räumliche Komplexität) und verkürzt die Ausführungszeit von Berechnungen (zeitliche Komplexität).

Sie können die gerade erstellte dünne Matrix in Berechnungen verwenden, als wäre es eine normale Matrix.

Erstellen Sie beispielsweise eine quadratische Matrix M mit vier Zeilen und vier Spalten.

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Muliplizieren Sie dann die Matrix M mit einer Einheitsmatrix der Größe 4.

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Muliplizieren Sie jetzt dieselbe Matrix M mit einer dünnen Einheitsmatrix der Größe 4.

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Wie Sie sehen, ist das Endergebnis der Operationen M*eye(4) und M*speye(4) immer dasselbe.

Jedoch erzielen Sie in der Operation mit der dünnen Matrix M*speye(4) das Ergebnis schneller und unter Verwendung einer geringeren Menge an Computerspeicher.

Dünne Diagonalmatrix

In Matlab gibt es eine spezifische Funktion, um dünne Diagonalmatrizen zu erstellen. Diese Funktion heißt spdiags().

spdiags(v,i,r,c)

• Der erste Parameter (v) ist ein Spaltenvektor mit den Elementen, die auf der Diagonale platziert werden sollen
• Der zweite Parameter (i) ist der Index der Diagonale, auf der Sie die Elemente platzieren möchten. Standardmäßig ist es 0, wobei Null die Hauptdiagonale ist)
• Die dritte (r) und vierte (c) Parameter sind die Anzahl der Zeilen und Spalten der zu erstellenden dünnen Matrix

Geben Sie beispielsweise spdiags([1;2;3],0,3,3) ein, um eine dünne Diagonalmatrix der Größe 3x3 zu erstellen.

>> spdiags([1;2;3],0,3,3)
ans =
Komprimierte Spaltendünne Matrix (Zeilen = 3, Spalten = 3, nnz = 3 [33%])

(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

Matlab platziert die Elemente des Vektors [1;2;3] auf der Hauptdiagonale einer 3x3-Matrix.

Das resultierende Ergebnis ist eine dünne Matrix der Diagonalmatrix

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

Erstellung einer Sparse-Matrix Schritt für Schritt

In Matlab lässt sich eine Sparse-Matrix dadurch definieren, dass man die Positionen aller Nicht-Null-Elemente in der Matrix angibt.

Betrachten Sie zum Beispiel die Erstellung einer Sparse-Matrix anhand dieser Matrix:

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Zur Definition der Sparse-Matrix tragen Sie die Nicht-Null-Werte in ein Array ein, wobei Sie jeweils die Zeilen- und Spaltennummer sowie den Wert selbst angeben.

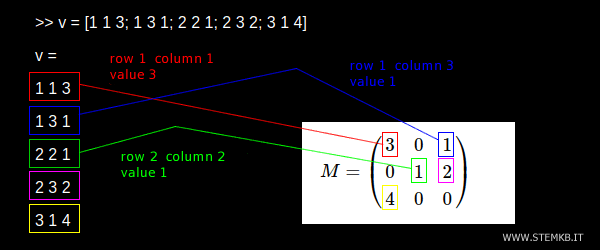
>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Jede Zeile dieses Arrays verweist auf die Position (Zeile und Spalte) eines Nicht-Null-Elements der Matrix und dessen Wert.

Das erste Nicht-Null-Element (3) befindet sich beispielsweise in der ersten Zeile und ersten Spalte (1,1), wie im folgenden Beispiel in Rot dargestellt. Um dieses Element in der Sparse-Matrix zu kennzeichnen, tragen Sie '1 1 3' in eine Zeile des Arrays ein. Und so weiter.

Nachdem Sie das Array mit den Nicht-Null-Werten definiert haben, erstellen Sie die Sparse-Matrix mithilfe der Funktion spconvert().

>> spconvert(v)

Das Resultat ist eine Sparse-Matrix, in der die Werte an den von Ihnen festgelegten Positionen stehen.

ans =
Compressed Column Sparse (Zeilen = 3, Spalten = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

Beim Erstellen des Arrays sind Sie in der Reihenfolge der Nicht-Null-Elemente flexibel.

Es ist auch möglich, dieselbe Matrixposition mehrfach mit unterschiedlichen Werten zu definieren.

Bitte beachten Sie, dass Matlab bei mehrfacher Definition derselben Position in einem Array die Werte summiert. Wenn Sie beispielsweise in einer Sparse-Matrix die Werte 2 und 3 an der Position (1,1) angeben, betrachtet Matlab die Summe der beiden Werte als 2+3=5 an dieser Position.

Diese Methode ermöglicht es Ihnen auch, Sparse-Matrizen mit komplexen Zahlen zu erstellen.