Grenzwertberechnung einer Funktion in Octave

In dieser Anleitung erfahren Sie, wie Sie in Octave den Grenzwert einer Funktion anhand praktischer Beispiele berechnen.

Voraussetzungen. Sie sollten die Open-Source-Software GNU Octave bereits auf Ihrem Computer installiert haben, einschließlich des Symbolic-Moduls.
Die grafische Benutzeroberfläche von Octave:

Beginnen Sie mit der Definition der unabhängigen Variable x mittels des Befehls syms in der Octave-Befehlszeile:

syms x

Um den Grenzwert der Funktion f(x)=(x+1)/(x-1) für x→∞ zu berechnen, verwenden Sie:

$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$

Geben Sie den Befehl limit() ein.

Geben Sie den Funktionsnamen f(x) als ersten Parameter und den Variablennamen x als zweiten Parameter ein. Drücken Sie dann die Eingabetaste.

limit((x+1)/(x-1),x)

Octave liefert als Ergebnis:

ans = (sym) 1

Das bedeutet, der Grenzwert der Funktion für x→∞ ist 1.

Der Grenzwert der Funktion f(x)=(x+1)/(x-1) für x→∞ ist 1. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$ 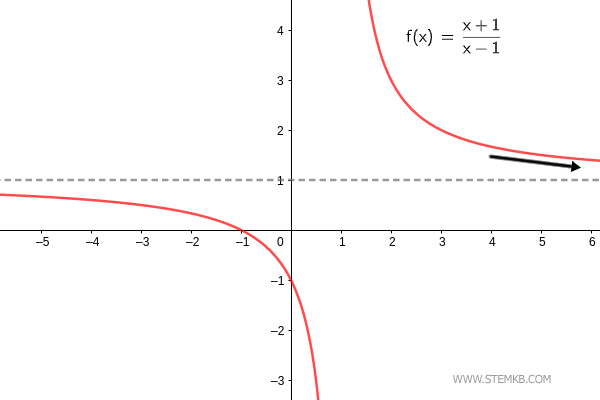Grafik der Funktion, wenn x gegen Unendlich geht.

Für x→-∞ fügen Sie `-inf` als dritten Parameter hinzu:

limit((x+1)/(x-1),x,-inf)

Auch hier ist das Ergebnis 1.

ans = (sym) 1

Der Grenzwert der Funktion f(x)=(x+1)/(x-1) für x→-∞ ist 1. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$ 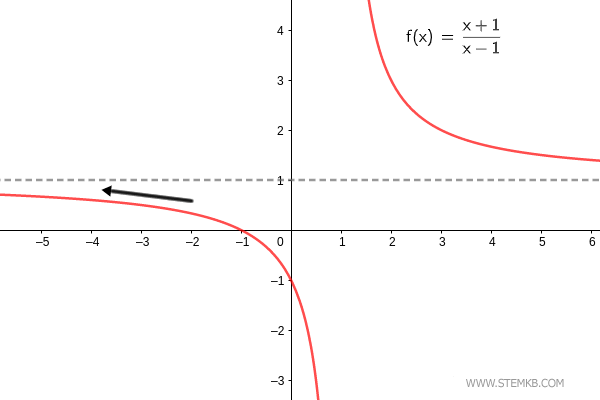Grafik der Funktion, wenn x gegen minus Unendlich geht.

Wenn Sie den Grenzwert für ein bestimmtes x₀ berechnen möchten, geben Sie x₀ als dritten Parameter an. Zum Beispiel für x → 2

limit((x+1)/(x-1),x,2)

Das Ergebnis in diesem Fall ist 3.

ans = (sym) 3

Der Grenzwert der Funktion f(x)=(x+1)/(x-1) für x→2 ist 3. $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$ 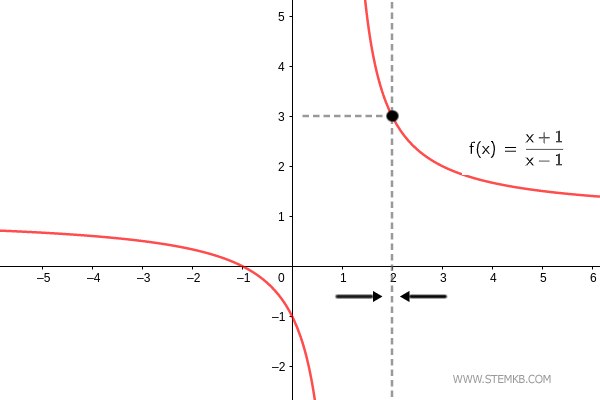Grenzwert der Funktion, wenn x gegen 2 geht.

Für den rechtsseitigen Grenzwert bei x→1⁺ verwenden Sie den Befehl:

limit((x+1)/(x-1),x,1,'right')

Das Ergebnis ist Unendlich (∞).

ans = (sym) ∞

Der Grenzwert der Funktion f(x)=(x+1)/(x-1) für x→1⁺ ist Unendlich. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$ 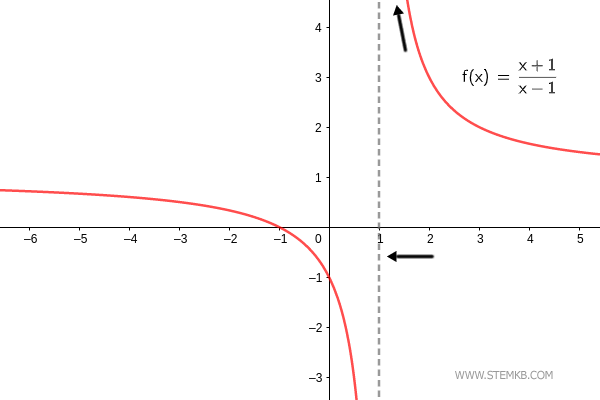Rechtsseitiger Grenzwert der Funktion, wenn x sich der Eins nähert.

Für den linksseitigen Grenzwert bei x→1^- lautet der Befehl:

limit((x+1)/(x-1),x,1,'left')

Hier ist das Ergebnis minus Unendlich (-∞).

ans = (sym) -∞

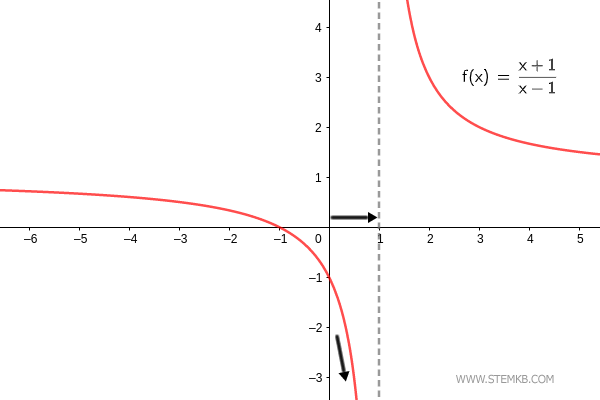
Der Grenzwert der Funktion f(x)=(x+1)/(x-1) für x→1^- ist minus Unendlich. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$
Linksseitiger Grenzwert der Funktion, wenn x sich der Eins nähert.

Wir hoffen, dass diese Anleitung Ihnen weitergeholfen hat. Für weitere Tipps und Anleitungen zu Octave bleiben Sie uns gerne weiterhin verbunden.