Eine Matrix in Octave spiegeln

In dieser Lektion möchte ich Ihnen zeigen, wie Sie eine Matrix in Octave horizontal oder vertikal spiegeln können. Dies ist ein grundlegender Aspekt der linearen Algebra und eine häufig verwendete Operation in vielen Bereichen der Mathematik und Datenanalyse.

Aber was genau bedeutet es, eine Matrix zu spiegeln? Im Grunde genommen handelt es sich dabei um eine Transformation, bei der die Matrix entlang einer Achse "gespiegelt" wird. Dabei wird die Reihenfolge der Zeilen oder Spalten umgekehrt. Wenn wir zum Beispiel eine Matrix horizontal spiegeln, kehren wir die Reihenfolge der Spalten um. Die erste Spalte wird zur letzten und umgekehrt.

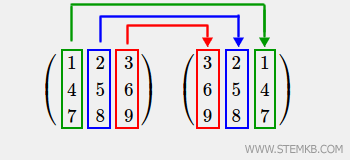
Wenn wir hingegen eine Matrix vertikal spiegeln, kehren wir die Reihenfolge der Zeilen um. Die erste Zeile wird zur letzten und umgekehrt.

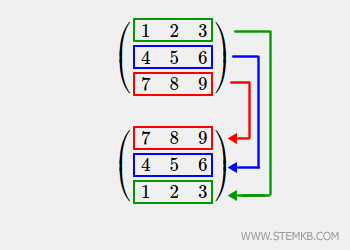
Lassen Sie uns das an einem praktischen Beispiel verdeutlichen.

Erstellen Sie zunächst eine 3x3-Matrix mit drei Zeilen und drei Spalten.

>> M=[1 2 3; 4 5 6; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

Um die Matrix horizontal zu spiegeln, müssen Sie die Reihenfolge der Spalten von links nach rechts umkehren.

Geben Sie dazu fliplr(M) ein:

>> fliplr(M)
ans =
3 2 1
6 5 4
9 8 7

Das Ergebnis ist eine Matrix, bei der die Reihenfolge der Spalten umgekehrt ist. Die dritte Spalte wird zur ersten und umgekehrt.

Um die Matrix vertikal zu spiegeln, müssen Sie die Reihenfolge der Zeilen von oben nach unten umkehren.

Geben Sie dazu flipud(M) ein:

>> flipud(M)
ans =
7 8 9
4 5 6
1 2 3

Das Ergebnis ist eine Matrix, bei der die Reihenfolge der Zeilen umgekehrt ist.

Die erste Zeile wird zur dritten und umgekehrt.