Extraktion aller Diagonalen aus einer Matrix in Octave

In dieser Lektion möchten wir uns damit befassen, wie alle Diagonalen einer Matrix in Octave extrahiert werden können. Dabei werden wir einen praktischen Ansatz verfolgen.

Zunächst einmal, was sind die Diagonalen einer Matrix? Vereinfacht ausgedrückt handelt es sich dabei um die Elemente, die entlang der Diagonalen liegen, welche im oberen rechten Eck beginnen und im unteren linken enden, und natürlich auch umgekehrt. So setzt sich zum Beispiel die Hauptdiagonale der folgenden Matrix aus den Elementen 1, 5 und 9 zusammen. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$ Die Nebendiagonale hingegen enthält die Elemente 3, 5 und 7. $$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$

Lassen Sie uns dies nun anhand eines praktischen Beispiels verdeutlichen.

Zuerst erstellen wir eine 3x3 Matrix.

>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

Um sämtliche Diagonalen zu extrahieren, geben Sie den Befehl spdiags() ein:

>> spdiags(M)
ans =
7 4 1 0 0
0 8 5 2 0
0 0 9 6 3

Jede Spalte der resultierenden Matrix repräsentiert eine Diagonale der Ursprungsmatrix M.

Die mittlere rote Spalte bildet dabei die Hauptdiagonale ab, welche aus den Zahlen 1, 5, 9 besteht.

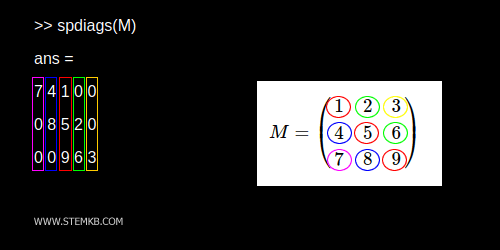
Wenn Sie nur die Hauptdiagonale extrahieren möchten, nutzen Sie den Befehl spdiags(M,0)

>> spdiags(M,0)
ans =
1
5
9

Um die Diagonale über der Hauptdiagonale zu extrahieren, verwenden Sie spdiags(M,1)

>> spdiags(M,1)
ans =
0
2
6

Um die Diagonale unter der Hauptdiagonale zu extrahieren, verwenden Sie spdiags(M,-1)

>> spdiags(M,-1)
ans =
4
8
0

Für die Extraktion aller Nebendiagonalen der Matrix M kombinieren Sie die Funktionen spdiags() und fliplr().

Die Funktion fliplr dreht die Matrix M von links nach rechts.

Geben Sie ein: spdiags(fliplr(M))

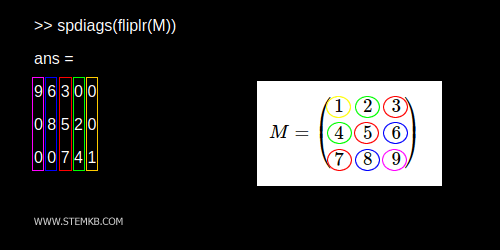
>> spdiags(fliplr(M))
ans =
9 6 3 0 0
0 8 5 2 0
0 0 7 4 1

Jede Spalte der Matrix repräsentiert nun eine Diagonale der Matrix von links nach rechts.

Die zentrale rote Spalte entspricht der Nebendiagonalen der Matrix, die aus den Zahlen 3, 5, 7 besteht.

Auf diese Weise können Sie jegliche Diagonale der Matrix extrahieren.