Dünnbesetzte Matrix in Octave

In dieser Online-Lektion erkläre ich Ihnen, wie man in Octave eine Sparse-Matrix erstellt. In der numerischen Mathematik bezeichnet man als dünnbesetzte oder schwachbesetzte Matrix

Was ist eine Sparse-Matrix und wozu dient sie? Wenn Sie eine sehr große Matrix mit vielen Nullen erstellen, belegen Sie unnötigerweise einen großen Teil des Arbeitsspeichers des Computers. Zum Beispiel hat eine Diagonalmatrix nur auf der Hauptdiagonale Nicht-Null-Werte und sonst überall Nullen.$$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ Sie können das gleiche Ergebnis erzielen, indem Sie eine Sparse-Matrix erstellen, in der die Nullen komprimiert sind. So sparen Sie Speicherplatz.

Sparse-Matrizen können verwendet werden, um Einheitsmatrizen und komprimierte Diagonalmatrizen zu erstellen.

Die Sparse-Einheitsmatrix

Ich möchte Ihnen ein praktisches Beispiel geben.

Geben Sie eye(4) ein, um eine Einheitsmatrix zu erstellen.

>> eye(4)
ans =
Diagonal Matrix1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

In der Matrix gibt es 12 Nullen und 4 Einsen. Ein großer Teil des Raums wird unnötigerweise durch Nullwerte belegt.

Sie können die gleiche Einheitsmatrix mit der Sparse-Matrix-Technik erstellen, indem Sie den Befehl speye(4) verwenden

>> speye(4)
ans =
Compressed Column Sparse (rows = 4, cols = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

Die Sparse-Matrix speichert nur die Positionen (Zeile, Spalte), an denen Nicht-Null-Werte vorhanden sind, was weniger Speicherplatz benötigt.

Deshalb wird sie eine "Sparse"-Matrix genannt.

Anmerkung. Nur nützliche Informationen werden in der Sparse-Matrix gespeichert. In einer Einheitsmatrix sind Nullwerte irrelevant. Daher werden sie eliminiert. Dies reduziert den belegten Speicherplatz und beschleunigt die Matrixberechnung, insbesondere wenn die Matrix sehr groß ist.

Sie können die gerade erstellte Sparse-Matrix in Ihren Berechnungen verwenden, als wäre es eine 4x4-Einheitsmatrix.

Zum Beispiel, erstellen Sie eine Matrix mit 4 Spalten

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Nun multiplizieren Sie die Matrix M mit der Einheitsmatrix

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Dann multiplizieren Sie die M-Matrix mit der Sparse-Einheitsmatrix

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Das Ergebnis ist das gleiche.

Im zweiten Fall haben Sie weniger Speicher belegt und die Berechnungszeit ist kürzer.

Die Sparse-Diagonalmatrix

Verwenden Sie spdiags(), um eine Sparse-Diagonalmatrix mit Werten ungleich 1 zu erstellen

>> spdiags([1;2;3],0,3,3)
ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 3 [33%])

(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

• Der erste Parameter ist ein Spaltenvektor [1; 2; 3] mit den Elementen der Diagonalen
• Der zweite Parameter ist die Indexnummer der Diagonalen, wobei die Zahl Null (0) die Hauptdiagonale ist
• Der dritte und vierte Parameter sind die Anzahl der Zeilen (3) und Spalten (3) der Sparse-Matrix

Das Ausgabergebnis ist die Sparse-Matrix einer 3x3-Diagonalmatrix

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

Erstellen Sie eine Sparse-Matrix, indem Sie nur die Nicht-Null-Werte angeben

Sie können auch eine Sparse-Matrix erstellen, indem Sie nur Nicht-Null-Werte und deren Position in der Matrix angeben.

Zum Beispiel, erstellen Sie eine Sparse-Matrix mit diesen Werten

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Definieren Sie ein Array mit so vielen Zeilen wie Nicht-Null-Werte im Array vorhanden sind.

Schreiben Sie die Zeilennummer, die Spaltennummer und den Nicht-Null-Elementwert in jede Zeile des Arrays.

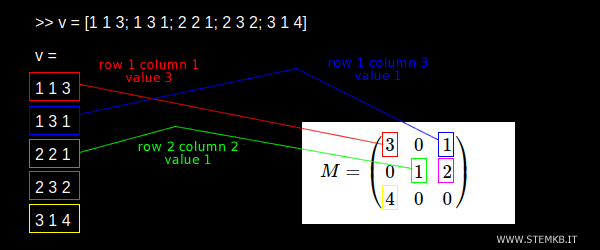
>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Anmerkung. Das erste Nicht-Null-Element (3) befindet sich in der ersten Zeile und Spalte (1,1). Daher ist die erste Zeile des Vektors 1 1 3. Das zweite Nicht-Null-Element (1) befindet sich in der ersten Zeile in der dritten Spalte. Daher ist die zweite Zeile des Vektors 1 3 1. Das dritte Nicht-Null-Element (2) befindet sich in der zweiten Zeile in der zweiten Spalte. Daher ist die dritte Zeile des Vektors 2 2 2. Und so weiter.

Um die Sparse-Matrix zu erstellen, verwenden Sie die Funktion spconvert()

>> spconvert(v)

Das Ergebnis ist eine Sparse-Matrix mit den Werten an den von Ihnen angegebenen Positionen.

ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

In dem Array, das Sie zum Erstellen der Sparse-Matrix verwendet haben, können Sie die Nicht-Null-Werte in beliebiger Reihenfolge definieren.

Anmerkung. Sie können auch mehrere Werte für dieselbe Position in der Matrix angeben. Wenn eine Position im Array mehrfach im Array vorhanden ist, addiert Octave die Werte zusammen, ohne einen Fehler zu erzeugen. Zum Beispiel, definieren Sie eine Sparse-Matrix, indem Sie an Position (1,1) den Wert 2 und den Wert 3 angeben. An Position (1,1) addiert Octave die beiden Werte 2 + 3 = 5.

Mit dieser Methode können Sie auch eine Sparse-Matrix mit komplexen Zahlen erstellen.