Die Rotation einer Matrix in Octave

In dieser Lektion möchte ich Ihnen zeigen, wie Sie eine Matrix in Octave auf effiziente Weise rotieren können. Ich werde dies anhand einiger praktischer Beispiele verdeutlichen.

Zunächst einmal, was genau bedeutet es, eine Matrix zu rotieren? Eine Matrix kann entweder im Uhrzeigersinn (nach rechts) oder gegen den Uhrzeigersinn (nach links) rotiert werden. Wenn Sie beispielsweise eine Matrix um 90 Grad im Uhrzeigersinn drehen, erhalten Sie folgendes Ergebnis. Lassen Sie uns dies an einem Beispiel verdeutlichen.

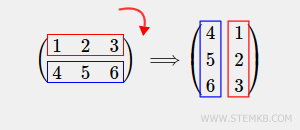
Beginnen wir mit der Erstellung einer 2x3 rechteckigen Matrix:

>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6

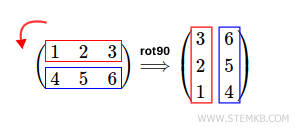
Jetzt wollen wir diese Matrix um 90 Grad gegen den Uhrzeigersinn drehen.

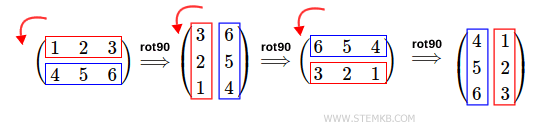
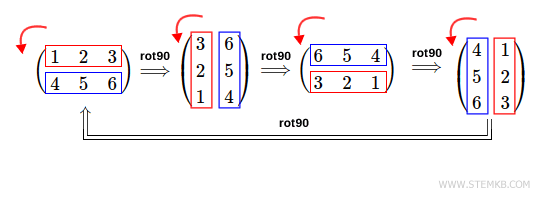
Dazu geben wir folgenden Befehl ein: rot90(M,1)

>> rot90(M,1)
ans =
3 6
2 5
1 4

Das Ergebnis ist eine 90-Grad-Drehung der Ausgangsmatrix nach links.

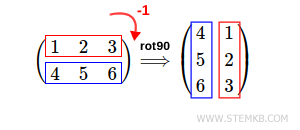
Ein wichtiger Hinweis: Sie können auch einfach rot90(M) eingeben, da Octave standardmäßig den zweiten Parameter auf 1 setzt. Die Standardrichtung ist gegen den Uhrzeigersinn (nach links), da dies die übliche Konvention in Mathematik und Physik ist. Um die Matrix nach rechts zu drehen, müssen Sie hingegen eine negative Zahl angeben, beispielsweise -1.

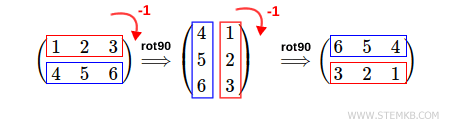
Wenn Sie die Matrix um 90 Grad nach rechts drehen möchten, geben Sie folgendes ein: rot90(M, -1).

Hierbei ist der zweite Parameter eine negative Ganzzahl, nämlich -1.

>> rot90(M,-1)
ans =
4 1
5 2
6 3

Dieses Mal haben wir die Matrix um 90 Grad nach rechts gedreht.

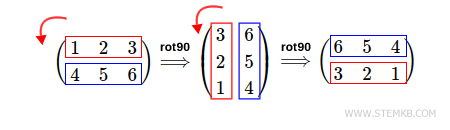
Sie können die Matrix auch um 180 Grad nach links drehen.

In diesem Fall geben Sie rot90(M,2) ein

>> rot90(M,2)
ans =
6 5 4
3 2 1

Das Ergebnis ist eine doppelte 90-Grad-Drehung der Matrix nach links.

Auf ähnliche Weise können Sie die Matrix um 180 Grad nach rechts drehen, indem Sie rot90(M, -2) eingeben.

Hierbei ist der zweite Parameter wieder eine negative Ganzzahl, nämlich -2.

>> rot90(M,-2)
ans =
6 5 4
3 2 1

Das Ergebnis ist eine doppelte 90-Grad-Drehung der Matrix nach rechts.

Mit der Funktion rot90(M, n) können Sie die Matrix beliebig oft drehen.

Der zweite Parameter gibt die Anzahl der Drehungen nach links (n> 0) oder nach rechts (n <0) an.

Zum Beispiel, um die Matrix um 270 Grad nach links zu drehen, geben Sie rot90(M,3) ein:

>> rot90(M,3)
ans =
4 1
5 2
6 3

Das Ergebnis ist eine dreifache 90-Grad-Drehung der Matrix nach links.

Um die Matrix um 270 Grad nach rechts zu drehen, geben Sieeinfach rot90(M, -3) ein und setzen -3 als zweiten Parameter der Funktion.

Um die Matrix um 360 Grad nach links zu drehen, geben Sie rot90(M,4) ein:

>> rot90(M,4)
ans =
1 2 3
4 5 6

In diesem Fall erhalten Sie die ursprüngliche Matrix zurück, da Sie vier 90-Grad-Drehungen nach links durchgeführt haben.

Ich hoffe, diese Anleitung hat Ihnen einen klaren Überblick über die Rotation von Matrizen in Octave gegeben.

Wie Sie sehen, ist es ein sehr mächtiges Werkzeug in der linearen Algebra, das eine Vielzahl von Anwendungen hat.