Wie man die Diagonalen einer Matrix in Octave austauscht

In dieser Lektion möchte ich Ihnen zeigen, wie Sie die Elemente auf einer Diagonale einer Matrix ersetzen können.

Zunächst einmal, was sind die Diagonalen einer Matrix? Sie sind die Elemente, die entlang der Linien liegen, die oben rechts beginnen und unten links enden und umgekehrt. Nehmen wir zum Beispiel die Hauptdiagonale der Matrix M, die aus den Elementen 1, 5, 9 besteht. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Lassen Sie uns das anhand eines praktischen Beispiels verdeutlichen.

Erstellen Sie zunächst eine 3x3-Matrix:

>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

Die Hauptdiagonale besteht aus den Elementen 1, 5, 9.

$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Um die Elemente der Hauptdiagonale durch -1, -2, -3 zu ersetzen, geben Sie spdiags([-1;-5;-9],0,M) ein

>> spdiags([-1;-5;-9],0,M)
ans =
-1 2 3
4 -5 6
7 8 -9

• Der erste Parameter ist ein Spaltenvektor [-1;-5;-9] mit den neuen Diagonalelementen.
• Der zweite Parameter (0) ist der Index der Diagonale. Die Hauptdiagonale hat den Index 0.

  Index 1 ist die Diagonale über der Hauptdiagonale, während Index -1 die Diagonale darunter ist.

• Der dritte Parameter M ist die Variable, in der die Matrix gespeichert ist.

Das Ergebnis ist eine quadratische Matrix mit den neuen Elementen auf der Hauptdiagonale.

$$ M = \begin{pmatrix} \color{red}{-1} & 2 & 3 \\ 4 & \color{red}{-5} & 6 \\ 7 & 8 & \color{red}{-9} \end{pmatrix} $$

Um die Elemente auf der Diagonale über der Hauptdiagonale zu ändern, geben Sie spdiags([-1;-5;-9],1,M) ein

>> spdiags([-1;-5;-9],1,M)
ans =
1 -5 3
4 5 -9
7 8 9

Die Funktion ersetzt die Elemente über der Hauptdiagonale.

$$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ 4 & 5 & \color{red}{-9} \\ 7 & 8 & 9 \end{pmatrix} $$

Beachten Sie, dass das erste Element -1 des Spaltenvektors [-1;-5;-9] nicht in der neuen Matrix erscheint, da es in diesem Fall außerhalb der Matrix liegt.

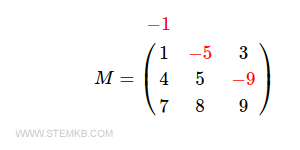
Um Elemente auf der sekundären Diagonale zu ersetzen, kombinieren Sie die Funktionen spdiags() und fliplr()

>> fliplr(spdiags([-1;-5;-9],0,fliplr(M)))
ans =
1 2 -1
4 -5 6
-9 8 9

Die Funktion ersetzt die Werte auf der sekundären Diagonale der Matrix.

Die sekundäre Diagonale beginnt oben rechts und endet unten links.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{-1} \\ 4 & \color{red}{-5} & 6 \\ \color{red}{-9} & 8 & 9 \end{pmatrix} $$

Auf diese Weise können Sie auch alle Werte auf den sekundären Diagonalen der Matrix ersetzen.