Die Transposition einer Matrix in Octave
In dieser Lektion möchte ich Ihnen zeigen, wie man in Octave eine Matrix transponiert.
Doch was genau ist eine transponierte Matrix? Bei der Transposition einer Matrix verwandeln wir jede Zeile in eine Spalte und umgekehrt. Nehmen wir beispielsweise die Matrix M mit zwei Zeilen und drei Spalten.
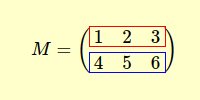
Die transponierte Matrix MT entsteht, indem wir die Elemente jeder Zeile als Spalte anordnen.
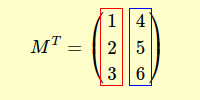
Lassen Sie mich Ihnen das anhand eines praktischen Beispiels verdeutlichen.
Stellen wir eine rechteckige Matrix mit sechs Elementen auf.
>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6
Unsere Matrix hat zwei Zeilen und drei Spalten.
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $$
Um die transponierte Matrix zu erzeugen, geben wir einfach den Variablennamen gefolgt von einem Apostroph ein: M'
>> M'
ans =
1 4
2 5
3 6
Es gibt auch eine weitere Methode, die Matrix zu transponieren, indem wir transpose(M) eingeben:
>> transpose(M)
ans =
1 4
2 5
3 6
In beiden Fällen erhalten wir die transponierte Matrix.
Die transponierte Matrix ist eine 3x2 rechteckige Matrix, bei der die Zeilen spaltenweise angeordnet sind.
$$ M^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} $$
Eine interessante Beobachtung: Die erste Zeile der Ausgangsmatrix bestand aus den Elementen [1 2 3]. In der transponierten Matrix bilden diese Elemente nun die erste Spalte. Dasselbe gilt für die zweite Zeile der Ausgangsmatrix. Die Zeile [4 5 6] ist in der transponierten Matrix die zweite Spalte.