Die polyfit()-Funktion in Matlab
Ich möchte Ihnen eine äußerst nützliche Funktion in Matlab vorstellen, die als polyfit() bekannt ist. Sie ermöglicht es Ihnen, ein Polynom zu ermitteln, das optimal zu einer gegebenen Datenserie passt.
polyfit(Y)
Der Parameter dieser Funktion ist ein Array, welches Ihre Daten enthält.
Betrachten wir beispielsweise folgende Datenserie:
>> X = [ 1 2 3 4 5 6 ]
>> Y = [ 3 8 6 9 7 8 ]
Um diese Datenserie grafisch darzustellen, nutzen Sie einfach die Funktion plot(X,Y).
>> plot(X,Y)
Dies resultiert in folgendem Graphen:
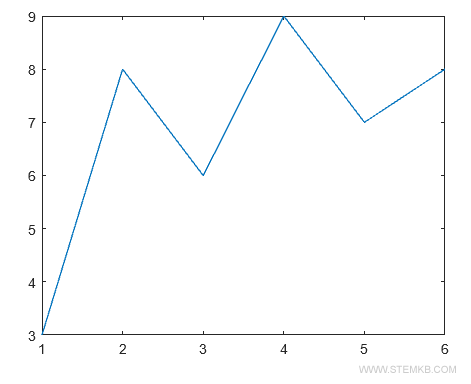
Möchten Sie nun ein Polynom ersten Grades finden, das diese Daten approximiert, verwenden Sie einfach polyfit(X,Y,1). Diese Funktion liefert Ihnen die Koeffizienten des gesuchten Polynoms.
>> P = polyfit(X,Y,1)
Das Ergebnis sieht wie folgt aus:
P =
0.71429 4.33333
Diese Zahlen sind die Koeffizienten des Polynoms ersten Grades:
$$ P_1(x) = 0.71429 \cdot x + 4.33333 $$
Mit der Funktion polyval() können Sie die Polynomwerte für jedes Element des X-Arrays berechnen. Diese Funktion benötigt die Polynomkoeffizienten und das Array X als Argumente.
>> polyval(P,X)
Das Ergebnis ist eine Reihe von Polynomwerten für jedes Element des X-Arrays:
ans =
5.0476 5.7619 6.4762 7.1905 7.9048 8.6190
Abschließend können Sie sowohl die ursprünglichen Daten als auch das berechnete Polynom mit der plot()-Funktion in einem Koordinatensystem darstellen.
plot(X,Y,X,polyval(P,X))
Das Polynom ersten Grades findet dabei eine Linie, die sich der Datenreihe annähert.
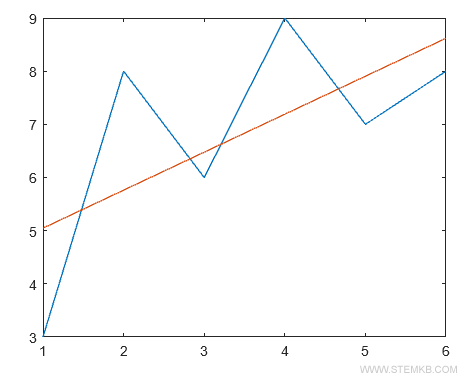
Beispiel 2
Angenommen, Sie möchten ein Polynom zweiten Grades finden, das besser zu den Daten passt.
In diesem Fall nutzen Sie dieselben Funktionen, jedoch mit dem Argument 2 anstelle von 1 in der polyfit()-Funktion.
>> P = polyfit(X,Y,2)
Damit erhalten Sie die Koeffizienten des Polynoms zweiten Grades, die Sie wiederum mit der polyval()-Funktion verwenden können, um die Werte des Polynoms für jedes Element des X-Arrays zu berechnen.
P =
-0.35714 3.21429 1.00000
Dies sind die Koeffizienten des Polynoms zweiten Grades.
$$ P_2(x) = -0.35714 \cdot x^2 + 3.214 29 x + 1.0 $$
Mit polyval(P,X) berechnen Sie die entsprechenden Polynomwerte.
>> polyval(P,X)
Das Ergebnis ist eine Werteserie für jedes Element des X-Arrays:
ans =
3.8571 6.0000 7.4286 8.1429 8.1429 7.4286
Wiederum können Sie die Daten und das Polynom in einem Koordinatensystem mit der plot()-Funktion visualisieren.
plot(X,Y,X,polyval(P,X))
Das Polynom zweiten Grades (in Rot dargestellt) liefert eine bessere Näherung an die Datenreihe.
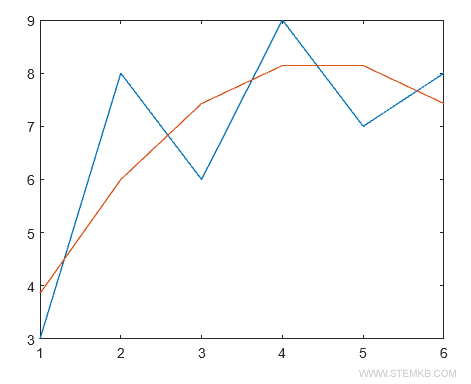
Beispiel 3
Zum Schluss können Sie denselben Vorgang wiederholen, um ein Polynom dritten Grades zu finden, das noch besser zu den Daten passt.
>> P = polyfit(X,Y,3)
Die Funktion liefert Ihnen folgendes Ergebnis:
P =
0.18519 -2.30159 9.08466 -3.66667
Diese Zahlen repräsentieren die Koeffizienten des Polynoms dritten Grades.
$$ P_3(x) = 0.18519x^3 -2.30159 \cdot x^2 + 9.08466 x - 3.66667 $$
Mit polyval(P,X) können Sie nun die entsprechenden Polynomwerte berechnen.
>> polyval(P,X)
Die Funktion generiert Polynomwerte für jedes Element des X-Arrays.
ans =
3.3016 6.7778 7.8730 7.6984 7.3651 7.9841
Zuletzt können Sie die Daten und das Polynom mit der plot()-Funktion graphisch darstellen.
plot(X,Y,X,polyval(P,X))
Das Polynom dritten Grades (in Rot) approximiert die Datenreihe noch genauer.
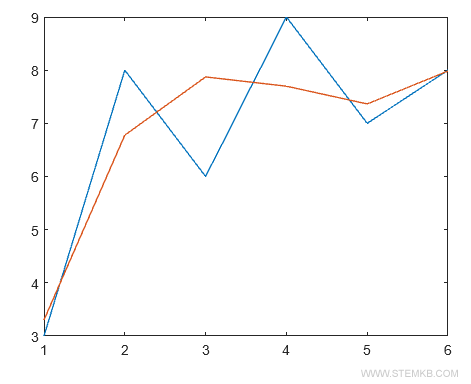
Je höher der Grad des Polynoms, desto genauer wird die Annäherung an die Datenreihe, da das Polynom die Datenserie immer besser repräsentiert. Somit ist polyfit() ein wertvolles Instrument, um das optimale Polynom für Ihre Daten in Matlab zu bestimmen.