Polynome in Matlab
Lassen Sie uns über Polynome in Matlab sprechen.
Was ist ein Polynom? Polynome sind Ausdrücke, die aus Konstanten und Variablen, oder Monomen, bestehen, welche ganze Zahlen als Exponenten haben und die durch grundlegende arithmetische Operationen (Addition, Subtraktion, Multiplikation und Division) kombiniert werden. Zum Beispiel ist dies ein Polynom vierten Grades. $$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$ Der Grad des Polynoms ist der höchste Exponent der Variablen x.
Wie man ein Polynom in Matlab definiert
Um nun ein Polynom in Matlab zu definieren, betrachten wir dieses Beispiel.
$$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$
Das Polynom hat nur eine unbekannte Variable (x).
Um es in Matlab zu verwenden, müssen Sie einen Vektor definieren, der die numerischen Koeffizienten der Terme enthält.
>> P = [1 2 -1 4 1]
Die Variable P ist ein Array mit den numerischen Koeffizienten des Polynoms P(x)=x4+2x3-x2+4x+1.
- Das erste Element des Arrays ist der Koeffizient 1 von x4
- Das zweite Element des Arrays ist der Koeffizient 2 von 2x3
- Das dritte Element des Arrays ist der Koeffizient -1 von -x2
- Das vierte Element des Arrays ist der Koeffizient 4 von 4x
- Das fünfte Element des Arrays ist der Koeffizient 1 von +1
Beachten Sie. Wenn ein Zwischengrad der Variablen fehlt, müssen Sie den Koeffizienten 0 einsetzen. Zum Beispiel fehlt in diesem Polynom x2 $$ P2(x)= x^3+2x-1 $$ In diesem Fall müssen Sie einen Array erstellen, indem Sie den Koeffizienten 0 an der zweiten Stelle einfügen.
>> P2 = [1 0 2 -1]
Nachdem Sie ihn erstellt haben, können Sie ihn verwenden, um die Werte des Polynoms P(x) zu berechnen, indem Sie die Variable x mit der Funktion polyval() variieren.
Zum Beispiel, um den Wert des Polynoms P(x) zu berechnen, wenn x=0, geben Sie polyval(P,0) ein.
>> polyval(P,0)
Matlab ersetzt den Wert Null für die unbekannte x und gibt das Ergebnis zurück.
In diesem Fall ist das Ergebnis 1
ans = 1
Überprüfen. Sie können schnell überprüfen, indem Sie x=0 im Polynom einsetzen $$ P(0) = x^4 + 2x^3 - x^2 + 4x +1 $$ $$ P(0) = (0)^4 + 2 \cdot 0^3 - 0^2 + 4 \cdot 0 +1 $$ $$ P(0)=1 $$ Das Ergebnis ist 1.
Ebenso können Sie den Wert des Polynoms P(x) berechnen, wenn x=1 ist, indem Sie polyval(P,1) eingeben.
>> polyval(P,1)
In diesem Fall ist das Ergebnis 7
ans = 7
Überprüfung. Um das Ergebnis zu überprüfen, setzen Sie x=1 in das Polynom ein $$ P(1) = x^4 + 2x^3 - x^2 + 4x +1 $$ $$ P(1) = (1)^4 + 2 \cdot 1^3 - 1^2 + 4 \cdot 1 +1 $$ $$ P(1)=1+2-1+4+1 $$ $$ P(1)=7 $$ Das Ergebnis ist 7.
Wenn Sie möchten, können Sie auch den Wert des Polynoms über einen Bereich von x-Werten berechnen.
Zum Beispiel tippen Sie x=0:5 um ein Array x mit den Werten von 0 bis 5 zu erstellen.
>> x=0:5
x =
0 1 2 3 4 5
Berechnen Sie nun die Werte des Polynoms im Bereich von 0 bis 5 mit der Funktion polyval(P,x)
>> polyval(P,x)
Die Funktion berechnet die Werte des Polynoms für jedes Element im Array x.
In diesem Fall ist das Ergebnis ein Array aus 6 Elementen.
ans =
1 7 37 139 385 871
Jedes Element ist der Wert des Polynoms im Intervall (0,5).
Hinweis. Das erste Element des Arrays ist P(0)=1 wenn x=0. Das zweite Element ist P(1)=7 wenn x=1. Das dritte Element ist P(2)=37. Das vierte Element ist P(3)=139. Und so weiter.
Die Verwendung von Arrays ermöglicht es Ihnen, jede Berechnung schnell durchzuführen.
Darüber hinaus erlauben sie auch die grafische Darstellung des Polynoms auf einer kartesischen Ebene mit der Funktion plot().
Geben Sie zum Beispiel diese Befehle nacheinander ein.
>> x=0:5;
>> P = [1 2 -1 4 1] ;
>> y=polyval(P,x);
>> plot(x,y);
Das Ergebnis ist der Graph des Polynoms im Intervall (0,5).
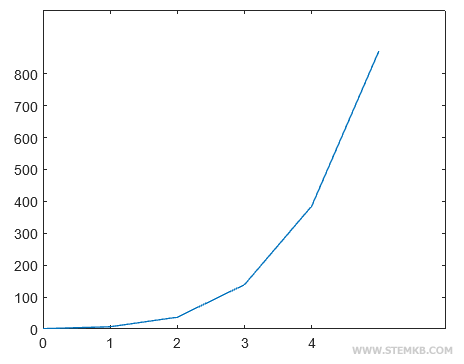
Auf der horizontalen Achse sind die Werte der unbekannten Variablen x abgetragen, während auf der vertikalen Achse die des Polynoms y.
Polynomoperationen
Mit Matlab können Sie Operationen mit Polynomen durchführen.
Lassen Sie mich Ihnen ein praktisches Beispiel geben.
Definieren Sie das Polynom x3+2x2+3 im Array P1
>> P1 = [ 1 2 0 3 ]
Definieren Sie dann das Polynom 2x3-x2+3x+1 im Array P2
>> P2 = [ 2 -1 3 1 ]
Führen Sie nun diese Operationen aus:
Addition
Um die beiden Polynome zu addieren, geben Sie P1+P2 ein
>> P1+P2
ans =
3 1 3 4
Das Ergebnis ist das Polynom 3x3+x2+3x+4
$$ P_1(x) + P_2(x) = (x^3+2x^2+3) + (2x^3-x^2+3x+1) $$ $$ P_1(x) + P_2(x) = x^3+ 2x^3+2x^2-x^2+3x+1+3 $$ $$ P_1(x) + P_2(x) = 3x^3+x^2+3x+4 $$
Subtraktion
Um die Differenz zwischen den Polynomen zu berechnen, geben Sie P1-P2 ein
>> P1-P2
ans =
-1 3 -3 2
Das Ergebnis ist das Polynom -x3+3x2-3x+2
$$ P_1(x) - P_2(x) = (x^3+2x^2+3) - (2x^3-x^2+3x+1) $$ $$ P_1(x) - P_2(x) = x^3- 2x^3+2x^2+x^2-3x+1-3 $$ $$ P_1(x) - P_2(x) = -x^3+3x^2-3x+2 $$
Multiplikation
Um das Produkt der Polynome P1·P2 zu berechnen, muss die Faltungsfunktion conv() verwendet werden
>> >> conv(P1,P2)
ans =
2 3 1 13 -1 9 3
Das Ergebnis ist das Polynom 2x6+3x5+x4+13x3-x2+9x+3
$$ P_1(x) \cdot P_2(x) = (x^3+2x^2+3) \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = x^3 \cdot (2x^3-x^2+3x+1) + 2x^2 \cdot (2x^3-x^2+3x+1) + \\ \ \ + 3 \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = 2x^6-x^5+3x^4+x^3 + 4x^5-2x^4+6x^3+2x^2 + \\ \ \ + 6x^3-3x^2+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+(4x^5-x^5)+(3x^4-2x^4)+(x^3 +6x^3+ 6x^3) + \\ \ \ + (2x^2-3x^2)+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+3x^5+x^4+13x^3 -x^2+9x+3 $$
Division
Um den Quotienten zweier Polynome zu berechnen, müssen Sie die Funktion deconv() verwenden
>> [q,r] = deconv(P1,P2)
q = 0.50000
r = 0.00000 2.50000 -1.50000 2.50000
Die Funktion deconv() gibt zwei Ergebnisse zurück:
- das Quotientenpolynom (q)
- das Restpolynom (r)
Das Ergebnis ist das Quotientenpolynom q=0,5
$$ Q = \frac{1}{2} $$
mit dem Rest r=2,5x2-1,5x+2,5
$$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$
Überprüfung. Führen Sie algebraische Berechnungen durch, um zu überprüfen, ob das Produkt korrekt ist. $$ P_1(x) : P_2(x) = \frac{x^3+2x^2+3}{2x^3-x^2+3x+1} $$ In diesem Fall ist die Berechnung etwas lang.
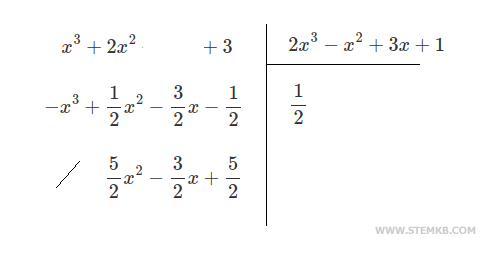
Das Quotientenpolynom ist $$ Q= \frac{1}{2} $$ mit dem Rest $$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ Multiplizieren Sie das Quotientenpolynom mit dem Divisorpolynom und addieren Sie den Rest: $$ Q \cdot (2x^3 -x^2+3x+1) + R $$ $$ \frac{1}{2} \cdot (2x^3 -x^2+3x+1) + \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 - \frac{1}{2} x^2+ \frac{3}{2}x+ \frac{1}{2}+ \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 + \frac{5-1}{2} x^2+ \frac{3-3}{2}x+ \frac{5+1}{2} $$ $$ x^3 + \frac{4}{2} x^2+ \frac{0}{2}x+ \frac{6}{2} $$ $$ x^3 + 2 x^2+ 3 $$ Das Ergebnis ist das Dividendenpolynom. Daher ist das Ergebnis der Division zwischen den beiden Polynomen korrekt.